SOLUTION: Can you help me to my question please? :( General Equation of Hyperbola with vertices (2,-1) and (2,-5) ; the Latus Rectum is 12

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Can you help me to my question please? :( General Equation of Hyperbola with vertices (2,-1) and (2,-5) ; the Latus Rectum is 12      Log On


   

Question 971243: Can you help me to my question please? :(
General Equation of Hyperbola
with vertices (2,-1) and (2,-5) ; the Latus Rectum is 12
Answer by Edwin McCravy(20059) About Me  (Show Source):
You can put this solution on YOUR website!
General Equation of Hyperbola
with vertices (2,-1) and (2,-5) ; the Latus Rectum is 12
We plot the two vertices and the center which is the midpoint
between them (2,-3), and sketch the hyperbola approximately, which must 
open up and down.



Since the hyperbola opens upward and downward, it has the equation:

%28y-k%29%5E2%2Fa%5E2-%28x-h%29%5E2%2Fb%5E2=1

The center is (h,k) = (2,-3), the midpoint between vertices, and 
a = 2, the distance between the center and a vertex.

So we have everything but b

%28y-k%29%5E2%2Fa%5E2-%28x-h%29%5E2%2Fb%5E2=1

%28y-%28-3%29%29%5E2%2F2%5E2-%28x-2%29%5E2%2Fb%5E2=1

%28y%2B3%29%5E2%2F4-%28x-2%29%5E2%2Fb%5E2=1

If you have studied the formula for the length of the
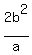latus rectum which is 2b%5E2%2Fa, we can use that to 
find b:

2b%5E2%2Fa=12
2b%5E2%2F2=12
b%5E2=12

we have the equation

%28y%2B3%29%5E2%2F4-%28x-2%29%5E2%2Fb%5E2=1
%28y%2B3%29%5E2%2F4-%28x-2%29%5E2%2F12=1

That's the standard equation.  The general equation can be 
gotten by multiplying through by LCD=12, squaring the
binomials and simplifying: 

x%5E2-3y%5E2-4x-18y-11=0

There is another way to get this answer if you haven't
studied the latus rectum formula.  Let me know in the 
thank-you note form below if you haven't studied that 
formula, and I'll show you how to find b without using 
it.

Edwin