 In the graph above, the green line is the latus rectum, the two red
points are the foci.
The distance between the foci is given as
In the graph above, the green line is the latus rectum, the two red
points are the foci.
The distance between the foci is given as  Since c is half the distance between foci,
Since c is half the distance between foci,  .
Since the latus rectum is given as 4, the y-coordinate of the
point at the top of the latus rectum is 2. So the coordinates
of the point at the top of the latus rectum are
.
Since the latus rectum is given as 4, the y-coordinate of the
point at the top of the latus rectum is 2. So the coordinates
of the point at the top of the latus rectum are 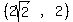 .
The equation of the ellipse is
(1)
.
The equation of the ellipse is
(1) 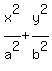

 Substituting that point:
Substituting that point:
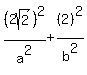


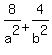

 (2)
(2) 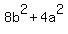

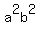 Since
Since  and
and 


 Substituting in (2)
Substituting in (2)
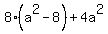

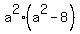
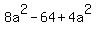

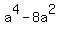
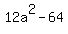

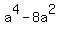
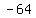

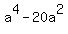


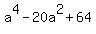


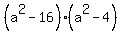


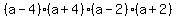 That has solutions a=4, a=-4, a=2, a=-2
The only one it can be is a=4
Substituting in
That has solutions a=4, a=-4, a=2, a=-2
The only one it can be is a=4
Substituting in 


 So the equation of the ellipse, substituting in (1),
So the equation of the ellipse, substituting in (1),
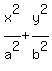


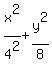


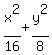

 Edwin
Edwin