Question 935298: how can I solve center,foci,eccentricity&latus rectum of ellipse
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you're asking about finding the length of the latus rectum of an ellipse, it is:
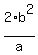
If you're asking about how to find the endpoints of the latus rectum, then- Determine if the ellipse is vertical or horizontal.
- Find the center, (
 , ,  ), of the ellipse. ), of the ellipse. - Find the "
 " for the ellipse. " " for the ellipse. " " is the distance from the center of the ellipse to each focus. " " is the distance from the center of the ellipse to each focus. " " is often found using the " " is often found using the " " and " " and " " from the equation of the ellipse and the equation " from the equation of the ellipse and the equation  - Find half of the length of the latus rectum. IOW:
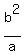 . We're going to call this number " . We're going to call this number " " in the next part. " in the next part. - The endpoints of the two latus rectum...
- for a horizontal ellipse: (
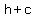 , , 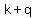 ), ( ), (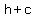 , , 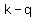 ), ( ), (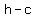 , , 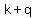 ) and ( ) and (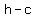 , , 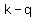 ) ) - for a vertical ellipse: (
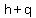 , , 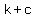 ), ( ), (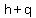 , ,  ), ( ), (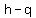 , , 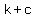 ) and ( ) and (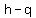 , , 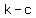
|
|
|