|
Question 923595: Find the equation of the parabola with vertex (-2,-1) & the equation of the directrix is x-2y+1=0?
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation of the parabola with vertex (-2,-1) & the equation of the directrix is x-2y+1=0?
 The black line is the given directrix.
The black point is the given focus.
The green line is the axis of symmetry, through the vertex
perpendicular to the directrix.
The red point is the focus, which we must find.
The point P(x,y) is an arbitrary point on the parabola.
By the definition of a parabola, the two blue lines (one from
P(x,y) to the focus and the other from P(x,y) to the directrix)
must be equal.
We find the perpendicular distance from the vertex to the directrix,
(the length oif the left blue line) by using the formula:
The perpendicular distance from the point P(x1,y1)
to the line Ax+y+C=0 is
d =
The black line is the given directrix.
The black point is the given focus.
The green line is the axis of symmetry, through the vertex
perpendicular to the directrix.
The red point is the focus, which we must find.
The point P(x,y) is an arbitrary point on the parabola.
By the definition of a parabola, the two blue lines (one from
P(x,y) to the focus and the other from P(x,y) to the directrix)
must be equal.
We find the perpendicular distance from the vertex to the directrix,
(the length oif the left blue line) by using the formula:
The perpendicular distance from the point P(x1,y1)
to the line Ax+y+C=0 is
d =  That gives d =
That gives d = 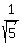 or or 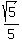 .
Then we find the focus, which is on the axis of symmetry a distance
of .
Then we find the focus, which is on the axis of symmetry a distance
of 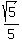 from the focus (or from the focus (or  from the directrix).
The focus turns out to be the point from the directrix).
The focus turns out to be the point  ,
Next we pick an arbitrary point on the parabola P(x,y).
We set its perpendicular distance to the directrix equal to its distance
from the focus (we are setting the two blue lines equal in length): ,
Next we pick an arbitrary point on the parabola P(x,y).
We set its perpendicular distance to the directrix equal to its distance
from the focus (we are setting the two blue lines equal in length):
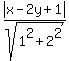  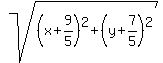 Simplify/square both sides and after much algebra you'll end up with the
equation:
Simplify/square both sides and after much algebra you'll end up with the
equation:
 If you get stuck on any step, you can contact me through the thank-you
note form below. You can come back online to this problem any time and
write something else in the thank-you note and I'll get back to you.
Edwin
If you get stuck on any step, you can contact me through the thank-you
note form below. You can come back online to this problem any time and
write something else in the thank-you note and I'll get back to you.
Edwin
|
|
|
| |