Question 914520: Identify the focus and directrix of the parabola y=-15x^2, 6x^2-3y=0, 2y^2+10x=0!?
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! y = -15x^2 , Parabola opening up(a>0) or down(a<0), 
C(0,0)
4p = 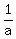 (Note: |4p| being the length of the latus rectum) (Note: |4p| being the length of the latus rectum)
p = 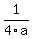 = -1/60, F(0, -1/60), Directrix y = 1/60 = -1/60, F(0, -1/60), Directrix y = 1/60

........
y = 2x^2 , Parabola opening up(a>0) or down(a<0), 
C(0,0)
p = 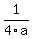 p = 1/8, F(0, 1/8), Directrix y = -1/8 p = 1/8, F(0, 1/8), Directrix y = -1/8

............
x = -.2x^2 Parabola opening right(a>0) or left(a<0), 
C(0,0)
p = 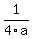 = -1/.8 = -1.25 F(-1.25 , 0), Directrix x = 1.25 = -1/.8 = -1.25 F(-1.25 , 0), Directrix x = 1.25

|
|
|