SOLUTION: I have a set of several of these: Sketch these curves. (Are they all hyperbolas? Explain.) {{{x^2 - y^2 = 10}}} How do I sketch these, and what makes a hyperbola a hyperbola

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: I have a set of several of these: Sketch these curves. (Are they all hyperbolas? Explain.) {{{x^2 - y^2 = 10}}} How do I sketch these, and what makes a hyperbola a hyperbola      Log On


   

Question 913718: I have a set of several of these:
Sketch these curves. (Are they all hyperbolas? Explain.)
x%5E2+-+y%5E2+=+10
How do I sketch these, and what makes a hyperbola a hyperbola?
I hate my textbook. It barely tells you how to do any of these.
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
There are many resources on the Internet, you're not stuck with only your textbook any more.
Hyperbolas have the general form of %28x%2Fa%29%5E2-%28y%2Fb%29%5E2=1
You sketch like you would for any function.
Pick an x, generate a y, plot the ordered pair.
With both variables being squared, you can save time using symmetry.
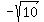Let y=0, x%5E2=10 x=0+%2B-+sqrt%2810%29
(sqrt%2810%29,0) and (-sqrt%2810%29},0)

Let y=2 and y=-2,
x%5E2-4=10
x%5E2=14
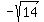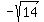x=0+%2B-+sqrt%2814%29
(2,sqrt%2814%29,(-2,sqrt%2814%29),(2,-sqrt%2814%29,(-2,-sqrt%2814%29)

.
.
.