SOLUTION: Identify the focus point and the equation of the directrix for the parabola defined by these equations I hope it's okay that I stick a couple of different scenarios, please explai

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Identify the focus point and the equation of the directrix for the parabola defined by these equations I hope it's okay that I stick a couple of different scenarios, please explai      Log On


   

Question 913711: Identify the focus point and the equation of the directrix for the parabola defined by these equations
I hope it's okay that I stick a couple of different scenarios, please explain how the answer is obtained. I don't even particularly need the answer; I have the answer key. I just don't know how to obtain said answer.
1. y+=+x%5E2 2. y+=+cx%5E2 3. y+-+5+=+%281%2F4%29%28x+%2B+3%29%5E2
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
the vertex form of a Parabola opening up(a>0) or down(a<0), y=a%28x-h%29%5E2+%2Bk
where(h,k) is the vertex and x = h is the Line of Symmetry
p = 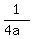1%2F%284a%29, where the focus is (h,k + p) and the Directrix y = (k - p)
1. y+=+x%5E2, V(0,0) a = 1, p = 1/(4a) , p = 1/4, F(0,.25) directrix y = -.25
2. y+=+cx%5E2, V(0,0) a = c, p = 1/(4c), F(0,1/(4c)) directrix y = -1/(4c)
3. y=+%281%2F4%29%28x+%2B+3%29%5E2+%2B+5V(-3,5),a = 1/4, p = 1/4a = 1, F(0,6) directrix y = 4