|
Question 895140: I cannot solve and graph the following parabola- y=-x^2+7.
Please show and explain the answer.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! set it equal to 0 and you get:
-x^2 + 7 = 0
subtract 7 from both sides and you get:
-x^2 = -7
multiply both sides by -1 and you get:
x^2 = 7
take the square root of both sides and you get:
x = plus or minus sqrt(7)
that's your solution.
plus or minus sqrt(7) are the values of x where the graph crosses the x-axis.
the graph crosses the x-axis when the value of y is equal to 0.
the two points where the graph crosses the x-axis are (-sqrt(7),0) and (sqrt(7),0).
the axis of symmetry will be between plus sqrt(7) and -sqrt(7).
this places it at x = 0.
you can also find the axis of symmetry by using the equation of x = -b/2a.
convert the equation to standard form of ax^2 + bx + c
you already have it because the equation is y = -x^2 + 7
a is the coefficient of the x^2 term and is equal to 1.
b is the coefficient of the x term and is equal to 0 because the x term is not there.
c is the constant term and is equal to 7.
you have:
a = 1
b = 0
c = 7
replace b with 0 and a with 7 and x = -b/2a becomes x = -0/2 which becomes x = 0.
the axis of symmetry is the vertical line at x = 0 which is the same as the y-axis.
since the quadratic equation is symmetric about the axis of symmetry, every x value that is equidistant from the axis of symmetry will have an equal y value.
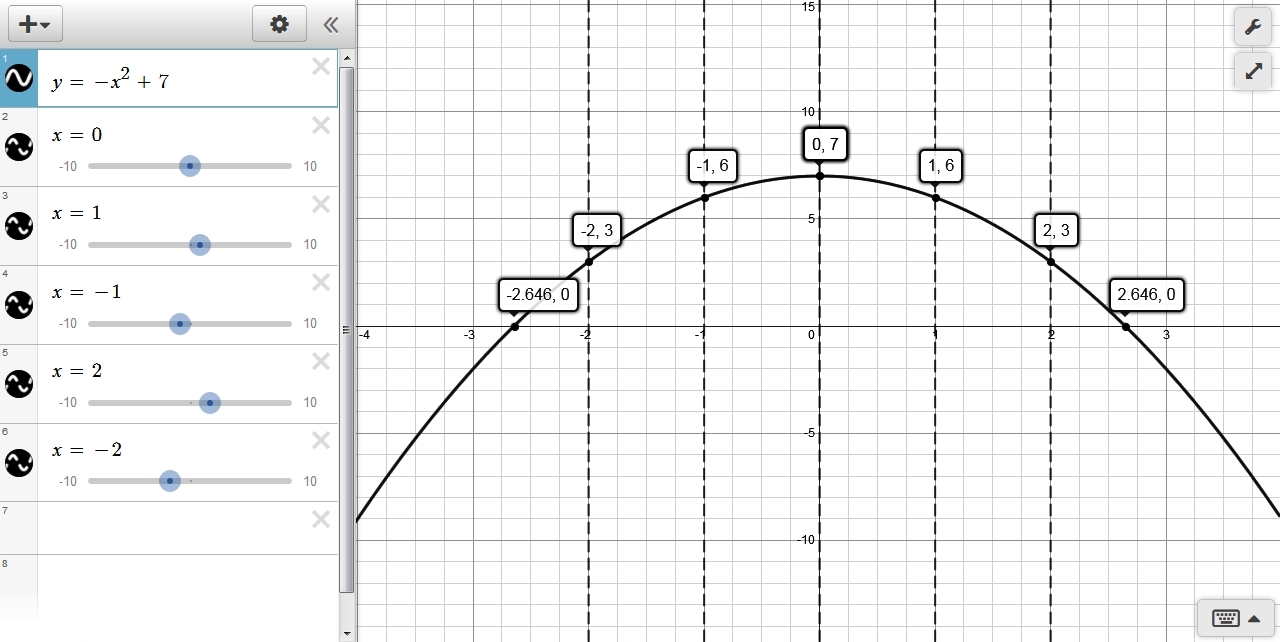
we'll plot x = plus or minus {sqrt(7),2,1,0} to show you what i mean.
your equation is y = -x^2 + 7
when x = plus or minue sqrt(7), y = 0
when x = plus or minus 2, y = 3
when x = plus or minus 1, y = 6
when x = 0, y = 7
note that plus or minus sqrt(7) is equal to plus or minus 2.646 rounded to 3 decimal places.
the graph of your equation looks like this:
|
|
|
| |