|
Question 880487: Imagine an elliptical orbit of a planet with a foci of F1 and F2. The ellipse is more wide then tall. The ellipse's center is at the origin. If a,b and c are all positive and all three variables are not equal to each other, which equation could represent the path of the planet. Provide an explanation
A)a(x^2)-b(y^2)=c^2
B)a(x^2)+b(y^2)=c^2
C)y=a(x^2)+(c^2)
D)(x^2)+(y^2)=c^2
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You ellipse would look like this: 
A)  <--> <--> is the equation of a hyperbola. is the equation of a hyperbola.
Since  and and 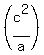 is always positive, is always positive,  can never be zero, so the curve always stays above the x-axis. can never be zero, so the curve always stays above the x-axis.

C)  <--> <--> is the equation of a parabola. is the equation of a parabola.
You can see that  , so it always stays above the x-axis. , so it always stays above the x-axis.
D)  <--> <--> is the equation of a circle. is the equation of a circle.
It is 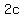 tall, extending from (0,-c) to (0,c), tall, extending from (0,-c) to (0,c),
and 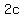 wide, extending from (-c,0) to (c,0). wide, extending from (-c,0) to (c,0).
B)  <--> <--> is the equation of an ellipse centered at the origin. is the equation of an ellipse centered at the origin.
It is 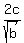 tall and tall and  wide. wide.
|
|
|
| |