Question 87147: 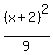 - - 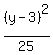 = 1 = 1
multi choice
a. (-2,-2)and (-2,8)
b. (-5,3)and (1,3)
c. (5,-3)and (-1,-3)
d. (2,2)and (2,-8)
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
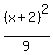 - - 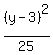 = 1
multi choice
a. (-2,-2)and (-2,8)
b. (-5,3)and (1,3)
c. (5,-3)and (-1,-3)
d. (2,2)and (2,-8)
You forgot to tell us what you are looking for!!!!!
I'm guessing you want the vertices. If so then
"b." is the correct choice, as you'll see below:
You'll have to learn all these things about
x-hyperbolas (ones that open right and left, so I'll
take this opportunity to explain all the parts of
x-hyperbolas.
(Note: y-hyperbolas (ones that open upward and downward,
are similar, except the y's and x's are reversed
throughout. If you need to know about them please
repost). = 1
multi choice
a. (-2,-2)and (-2,8)
b. (-5,3)and (1,3)
c. (5,-3)and (-1,-3)
d. (2,2)and (2,-8)
You forgot to tell us what you are looking for!!!!!
I'm guessing you want the vertices. If so then
"b." is the correct choice, as you'll see below:
You'll have to learn all these things about
x-hyperbolas (ones that open right and left, so I'll
take this opportunity to explain all the parts of
x-hyperbolas.
(Note: y-hyperbolas (ones that open upward and downward,
are similar, except the y's and x's are reversed
throughout. If you need to know about them please
repost).
 - -  = 1
is the equation of a hyperbola (two branches)
which opens right and left
which has center (h,k)
which has transverse axis = 2a
which has semi-transverse axis = a
which has which has vertices at the ends of the
transverse axis (h-a,k) and (h+a,k)
which has conjugate axis = 2b
which has semi-conjugate axis = b
which has ends of conjugate axis (h,k+b) and (h,k-b)
which has foci (h-c,k) and (h+c,k) where = 1
is the equation of a hyperbola (two branches)
which opens right and left
which has center (h,k)
which has transverse axis = 2a
which has semi-transverse axis = a
which has which has vertices at the ends of the
transverse axis (h-a,k) and (h+a,k)
which has conjugate axis = 2b
which has semi-conjugate axis = b
which has ends of conjugate axis (h,k+b) and (h,k-b)
which has foci (h-c,k) and (h+c,k) where  which has defining rectangle whose four corner points are
(h-a,k-b), (h-a,k+b), (h+a,k-b) and (h+a,k+b)
which has asymptotes whose equations are
which has defining rectangle whose four corner points are
(h-a,k-b), (h-a,k+b), (h+a,k-b) and (h+a,k+b)
which has asymptotes whose equations are
 and and  So your problem is
So your problem is
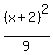 - - 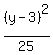 = 1
compare that with = 1
compare that with
 - -  = 1
and we see that h=-2, a=3, k=3, b=5
So your equation is the equation of a hyperbola (two branches)
which opens right and left
which has center (-2,3)
which has transverse axis = 2(3) = 6
which has semi-transverse axis = 3
which has which has vertices at the ends of the
transverse axis (-2-3,3) and (-2+3,3) or
(-5,3) and (1,3) [That's all you were asked for!]
which has conjugate axis = 2(5) = 10
which has semi-conjugate axis = 5
which has ends of conjugate axis (-2,3+5) and (-2,3-5)
or (-2,8) and (-2,-2)
which has vertices (-2-3,3) and (-2+3,3) or (-5,3) and (1,3)
which has foci (-2-c,3) and (-2+c,3) where = 1
and we see that h=-2, a=3, k=3, b=5
So your equation is the equation of a hyperbola (two branches)
which opens right and left
which has center (-2,3)
which has transverse axis = 2(3) = 6
which has semi-transverse axis = 3
which has which has vertices at the ends of the
transverse axis (-2-3,3) and (-2+3,3) or
(-5,3) and (1,3) [That's all you were asked for!]
which has conjugate axis = 2(5) = 10
which has semi-conjugate axis = 5
which has ends of conjugate axis (-2,3+5) and (-2,3-5)
or (-2,8) and (-2,-2)
which has vertices (-2-3,3) and (-2+3,3) or (-5,3) and (1,3)
which has foci (-2-c,3) and (-2+c,3) where  So
So  = =  , and the foci are
(-2- , and the foci are
(-2- ,3) and (-2+ ,3) and (-2+ ,3)
which has defining rectangle whose four corner points are
(-2-3,3-5), (-2-3,3+5), (-2+3,3-5) and (-2+3,3+5)
or
(-5,-2), (-5,8), (1,-2), and (1,8)
which has asymptotes whose equations are ,3)
which has defining rectangle whose four corner points are
(-2-3,3-5), (-2-3,3+5), (-2+3,3-5) and (-2+3,3+5)
or
(-5,-2), (-5,8), (1,-2), and (1,8)
which has asymptotes whose equations are
 and and  or
or
 and and 
 and and 
 and and 
 and and 
 and and  To get the graph, we plot the center, then the
transverse axis (which goes from vertex to vertex,
and the ends of the conjugate axes
To get the graph, we plot the center, then the
transverse axis (which goes from vertex to vertex,
and the ends of the conjugate axes
 Next we draw the defining rectangle:
Next we draw the defining rectangle:
 Next we draw AND EXTEND the diagonals of
the defining rectangle, which are the
asymptotes:
Next we draw AND EXTEND the diagonals of
the defining rectangle, which are the
asymptotes:
 Then finally we sketch in the hyperbola to
approach the asymptotes, and to just touch the
defining rectangle at the vertices (ends of
the transverse axes):
Then finally we sketch in the hyperbola to
approach the asymptotes, and to just touch the
defining rectangle at the vertices (ends of
the transverse axes):
 Edwin
Edwin
|
|
|