Question 861160: find the center (h,v) of the ellipse. show work
Center:(-3,0)
vertex1:(-3,5)
vertex2:(-3,-5)
focus1:(-3,4)
focus2:(-3,-4)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I see the answer to the question: Center:(-3,0) .
I also see information that would allow to find the center, and the equation of the ellipse.
I think someone typed the wrong question, and what should have been asked is "write the equation for the ellipse".
Form the coordinates of the vertices, you can find the coordinates (h,v) of the center.
The center is midway between the vertices, so averaging the coordinates of the vertices, you find the coordinates of the center:
 (averaging the x-coordinates of the vertices), (averaging the x-coordinates of the vertices),
and  (averaging the y-coordinates of the vertices). (averaging the y-coordinates of the vertices).
Form the coordinates of the foci, you can find the coordinates (h,v) of the center (also by averaging, the same way as done for the vertices).
You need all (or most) of that information to figure out the equation for the ellipse.
Your ellipse has the center, vertices, and foci on the vertical line  , and looks like this: , and looks like this:

The distance from the center to each vertex is usually called the "semi-major axis".
It is represented by the letter  , and in this case , and in this case  . .
The distance from the center to each focus is usually called the "focal distance", and is represented by the letter  . .
In this case  . .
There is another important quantity, often called the "semi-minor axis", represented by the letter  . .
The quantities  , ,  , and , and  are related by are related by

In this case, with  and and  , ,




When you know the coordinates of the center, (h,v),
know that the major axis is vertical
(center, vertices, and foci have the same x-coordinate),
and know 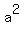 and and  , ,
you can write the equation of the ellipse as

In this case,
 ---> ---> 
|
|
|