SOLUTION: Find an equation for the hyperbola with foci (−3,−1) and (−3, 9) and asymptotes y = −3x/4 25/4 y = 3x/4 + 25/4 . Write your answer in the form (y-d)^2/a^2

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find an equation for the hyperbola with foci (−3,−1) and (−3, 9) and asymptotes y = −3x/4 25/4 y = 3x/4 + 25/4 . Write your answer in the form (y-d)^2/a^2       Log On


   

Question 852319: Find an equation for the hyperbola with foci (−3,−1) and (−3, 9) and asymptotes y = −3x/4 25/4 y = 3x/4 + 25/4 . Write your answer in the form (y-d)^2/a^2 -(x-c)^2/b^2 =1.
Not sure on how to approach this.
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi

foci (-3,-1) and (-3, 9) says it opens Up and Down C(-3, 4)the 4 halfway between %289+%2B+-1%29%2F2+=+4

Foci distance from center = 5   |5 = sqrt%28a%5E2%2Bb%5E2%29

slope  of asymptotes = ± 3/4 says b/a = 3/4  and  5 = 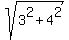sqrt%283%5E2%2B4%5E2%29

%28y-4%29%5E2%2F3%5E2+-+%28x%2B3%29%5E2%2F4%5E2%7C%5E2+=+1

 Standard Form of an Equation of an Hyperbola opening up and down is:

  %28y-k%29%5E2%2Fb%5E2+-+%28x-h%29%5E2%2Fa%5E2+=+1 with C(h,k) and vertices 'b' units up and down from center,  2b the length of the transverse axis

Foci sqrt%28a%5E2%2Bb%5E2%29units units up and down from ) ± b/a