Question 839121: 2 points are chosen on the parabola defined by y=x^2, one with a positive x-coordinate and the other with a negative x-coordinate. If the points are (a,b) and (c,d), where a < 0 and c > 0, find the y-intercept of the line joining the 2 points in terms of a and c
Found 2 solutions by stanbon, josmiceli:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2 points are chosen on the parabola defined by y=x^2, one with a positive x-coordinate and the other with a negative x-coordinate. If the points are (a,b) and (c,d), where a < 0 and c > 0, find the y-intercept of the line joining the 2 points in terms of a and c
--------
Points:
(a,b) implies b = a^2 because y = x^2
-----
(c,d) implies d = c^2 because y = x^2
-------------------------------
Using the two points (a,b) and (c,d)
slope = (d-b)(c-a)
---
Substituting for b and d you get:
= (c^2-a^2)/(c-a) = c+a
That is the slope.
------
Form of the line: y = mx + k where k is the y-intercept.
a^2 = (c+a)(a) + k
a^2 = ca+a^2 = k
k = -ca (that is the y-intercept)
====================================
Cheers,
Stan H.
==============
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Note that  must be must be 
or a positive number
-----------------------------
The given points are (a,b) and (c,d)
You are given that 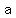 is negative is negative
and  is positive is positive
---------------------------------
For the 1st point, (a,b)
 , so I can say the point is , so I can say the point is
( a, a^2 )
For the 2nd point, ( c, d ),
 , so I can say the point is , so I can say the point is
( c, c^2 )
-----------------------------------
Using the general point slope formula:

Multiply both sides by 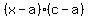




The y-intercept is 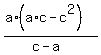 answer answer
check:
Let 
Let 


The points are ( -5,25 ) and ( 11, 121 )







This says the y-intercept is at 
check:





OK
|
|
|