SOLUTION: The equation is y^2=-13x It asks the find the foci and directrix and that axis is it on? Thank you for your help!!

 

Hi

BY DEFINITION

y^2=-13x Or   is a Parabola opening left along the x-axis 

See last Standard form Below

Vertex is (0,0), focus is (-13/4,0) and directrix is x = 13/4 (perpendicular line)







See below descriptions of various conics                         

Standard Form of an Equation of a Circle is  

where Pt(h,k) is the center and r is the radius



 Standard Form of an Equation of an Ellipse is  

where Pt(h,k) is the center. (a variable positioned to correspond with major axis)

 a and b  are the respective vertices distances from center

 and ±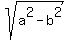are the foci distances from center: a > b



Standard Form of an Equation of an Hyperbola opening up and down is:

   with C(h,k) and vertices 'b' units up and down from center,  2b the length of the transverse axis

Foci units units up and down from center, along x = h

& Asymptotes Lines passing thru C(h,k), with slopes m =  ± b/a



Standard Form of an Equation of an Hyperbola opening right and  left is:

   with C(h,k) and vertices 'a' units right and left of center,   2a the length of the transverse axis

Foci are  units right and left of center along y = k

& Asymptotes Lines passing thru C(h,k), with slopes  m =  ± b/a 





the vertex form of a Parabola opening up(a>0) or down(a<0),  

where(h,k) is the vertex  and  x = h  is the Line of Symmetry

The standard form is , where  the focus is (h,k + p)



****the vertex form of a Parabola opening right(a>0) or left(a<0), 

 where(h,k) is the vertex and  y = k  is the Line of Symmetry

The standard form is , where  the focus is (h +p,k )