That's not enough information. You must be given something else,
because there are infinitely many ellipses with different
eccentricities 0 < e < 1 that have the same focus and directrix.
So you must be given something else besides what you posted.
There must be a way to determine the eccentricity, so that we
can set the ratio of the distance from an arbitrary point(x,y)
to the focus and directrix equal to that eccentricity. We
either have to be given the center, the other focus, a vertex
or some point that the graph passes through.
I'm going to suppose that you were given that the ellipse passes
through the point P( ,
,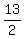 ). I picked that point
just because it works out fairly easier than some of the others.
You may be given some other information but I'll assume you were
given this point. If you were given a vertex, that will do, and
would actually be easier.
). I picked that point
just because it works out fairly easier than some of the others.
You may be given some other information but I'll assume you were
given this point. If you were given a vertex, that will do, and
would actually be easier.
 We can find the eccentricity by getting the ratio of the lengths of
those two green lines. First we find the distance
from that supposedly given point P(
We can find the eccentricity by getting the ratio of the lengths of
those two green lines. First we find the distance
from that supposedly given point P( ,
,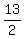 ) to the focus
by the distance formula:
) to the focus
by the distance formula:


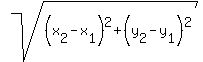


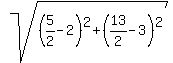


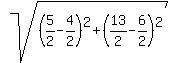


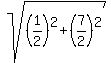


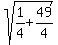


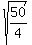


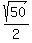


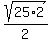


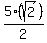 Then we find the distance from P(
Then we find the distance from P( ,
,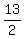 ) to the directrix
using the formula:
Perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is
d =
) to the directrix
using the formula:
Perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is
d = 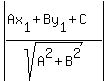 where the line is x+y+1=0 and the point is
(x1,y1) = P(
where the line is x+y+1=0 and the point is
(x1,y1) = P( ,
,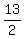 ), and
A=1, B=1, C=1
d =
), and
A=1, B=1, C=1
d =  d =
d = 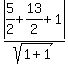 d =
d = 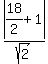 d =
d = 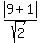 d =
d = 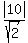 d =
d = 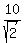 d =
d =  d =
d = 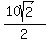 d = 5√2
So the eccentricity is
d = 5√2
So the eccentricity is 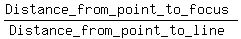

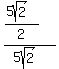

 So the eccentricity is
So the eccentricity is  , so we can go from there.
We let (x,y) be an arbitrary point on the graph:
, so we can go from there.
We let (x,y) be an arbitrary point on the graph:
 Now we will do the same thing with this arbitrary point (x,y) as we did
with the point P(
Now we will do the same thing with this arbitrary point (x,y) as we did
with the point P( ,
,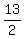 ) that I assumed that you were
given.
We find the distance from the arbitrary point (x,y) to the focus
by the distance formula:
) that I assumed that you were
given.
We find the distance from the arbitrary point (x,y) to the focus
by the distance formula:


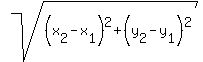


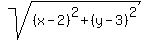 Then we find the distance from the arbitratrary point (x,y) to the
directrix using the same formula:
Perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is
d =
Then we find the distance from the arbitratrary point (x,y) to the
directrix using the same formula:
Perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is
d = 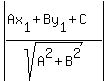 where the line is x+y+1=0 and this time the arbitrary point is
(x1,y1) = (x,y), and the same
A=1, B=1, C=1
d =
where the line is x+y+1=0 and this time the arbitrary point is
(x1,y1) = (x,y), and the same
A=1, B=1, C=1
d = 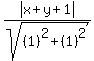 d =
d = 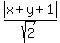 Then the ratio of the two distances equals the eccentricity
Then the ratio of the two distances equals the eccentricity 
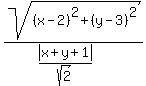

 Multiply both sides by
Multiply both sides by 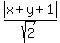
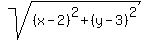


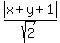 Multiply both sides by
Multiply both sides by 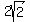
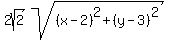

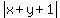 Square both sides:
Square both sides:
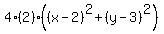


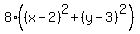


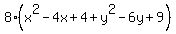

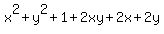
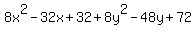

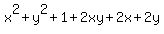 That simplifies to the equation:
That simplifies to the equation:
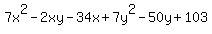

 Whatever the missing information was, the solution will be
similar to the above.
Edwin
Whatever the missing information was, the solution will be
similar to the above.
Edwin