y²-6y+48x²-3 = 0
You have to do algebraic operations on it to get it in the form:




 in which case it will look like this
in which case it will look like this  ,
or
,
or
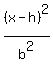

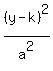

 in which case it will look like this
in which case it will look like this  We won't know which it is until later, when we can see which
denominator is larger, for the larger denominator will be "a²" and
the smaller denominator will be "b²".
y²-6y+48x²-3 = 0
Put the x term first, then the y terms second on the left
of the equation and isolate the number on the right:
48x²+y²-6y = 3
Since there is no x-term, all we have to do is write the
term 48x² as 48(x-0)².
48(x-0)²+y²-6y = 3
Since there is a y-term we must complete the square on
y²-6y:
To the side, we
1. Multiply the coefficient of y, which is -6, by
We won't know which it is until later, when we can see which
denominator is larger, for the larger denominator will be "a²" and
the smaller denominator will be "b²".
y²-6y+48x²-3 = 0
Put the x term first, then the y terms second on the left
of the equation and isolate the number on the right:
48x²+y²-6y = 3
Since there is no x-term, all we have to do is write the
term 48x² as 48(x-0)².
48(x-0)²+y²-6y = 3
Since there is a y-term we must complete the square on
y²-6y:
To the side, we
1. Multiply the coefficient of y, which is -6, by  ,
getting -3.
2. Square the result of step 1 (-3)² = 9
3. Add +9 to both sides of the equation
48(x-0)²+y²-6y+9 = 3+9
Then we factor y²-6y+9 as (y-3)(y-3) and then as (y-3)²
and replace y²-6y+9 by (y-3)². Combine the numbers on
the right side:
48(x-0)²+(y-3)² = 12
Then we divide through by 12 to get 1 on the right:
,
getting -3.
2. Square the result of step 1 (-3)² = 9
3. Add +9 to both sides of the equation
48(x-0)²+y²-6y+9 = 3+9
Then we factor y²-6y+9 as (y-3)(y-3) and then as (y-3)²
and replace y²-6y+9 by (y-3)². Combine the numbers on
the right side:
48(x-0)²+(y-3)² = 12
Then we divide through by 12 to get 1 on the right:
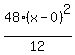

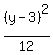


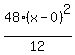

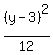

 We must get the 48 off the top of the first fraction.
To do that we divide top and bottom by 48:
We must get the 48 off the top of the first fraction.
To do that we divide top and bottom by 48:


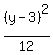

 Simplify:
Simplify:
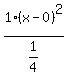

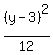


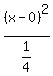

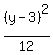

 Now we can tell that it is an ellipse that looks like this
Now we can tell that it is an ellipse that looks like this  because the larger denominator is a² which equals 12, and the
smaller denominator is b² which equals
because the larger denominator is a² which equals 12, and the
smaller denominator is b² which equals  So we compare it to:
So we compare it to:
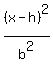

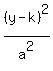

 (h,k) = (0,3) is the center,
Since a² = 12 then a = √12 = √4*3 = 2√ ≈ 3.46
Since b² =
(h,k) = (0,3) is the center,
Since a² = 12 then a = √12 = √4*3 = 2√ ≈ 3.46
Since b² =  then b =
then b =  =
=  a = the distance from the center (0,3) to the vertices, and b = the distance
from the center to the covertices. So we plot the center, the vertices,
which are a ≈ 3.46, units above and bellow the center, and the covertices
which are
a = the distance from the center (0,3) to the vertices, and b = the distance
from the center to the covertices. So we plot the center, the vertices,
which are a ≈ 3.46, units above and bellow the center, and the covertices
which are  of a unit right and left of the center:
of a unit right and left of the center:
 Then sketch in the ellipse (it's a tall skinny one!)
Then sketch in the ellipse (it's a tall skinny one!)
 Edwin
Edwin