x²+y²-4x+6y+1 = 0
We want to get it looking like this standard form
for a circle's equation:
(x-h)²+(y-k)² = r²
where the center is (h,k) and the radius is r
x²+y²-4x+6y+1 = 0
Swap the two middle terms to get the x-term next to
the 
-term and the 
-term next to the
y-term. Also add -1 to both sides:
x²-4x+y²+6y=-1
Complete the square on the first two terms:
1. Multiply the coefficient of x, which is -4, by 
getting -2
2. Square -2, getting (-2)² or 
.
3. Add to both sides:
x^2-4x+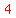
+y^2+6y = -1+
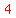Complete the square on the last two terms on the left:
1. Multiply the coefficient of y, which is 6, by
getting 3
2. Square 3, getting 
or 
.
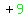3. Add 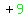to both sides:
1. Factor the trinomial consisting of the first three terms on the left.
2. Factor the trinomial consisting of the last three terms on the left.
3. Combine the numbers on the right.
Compare to
and the center is (h,k) = (2,-3) and the radius is r=
= 
= 
The graph is drawn with a compass, since it is a circle.
Put the sharp point of the compass at the center (2,-3):
Open the compass to 3.46 units, and draw this circle:
Answer: the center is (2,-3)
Edwin
