|
Question 824510: Hayden is the manager of a landscaping company. He had three employees to do the entire park, Cody Kaitlin and Joseph.Cody can complete the job in 8 hrs. kaitlin can complete the project in 6 hours. Joseph is neew so no one knows how it will take him. They must all work together to complete the project. How could I explain to Hayden how long it would take Joseph working by himself?
I saw the answer by one of your tutors, but not a solution!
Found 2 solutions by stanbon, KMST:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Hayden is the manager of a landscaping company. He had three employees to do the entire park, Cody Kaitlin and Joseph.
Cody can complete the job in 8 hrs.
Cody rate = 1/8 job/hr
-------------------------------
kaitlin can complete the project in 6 hours.
Kaitlin rate = 1/6 job/hr
-------------------------------
Joseph is new so no one knows how it will take him.
Joseph rate = 1/x job/hr
-------------------------------------
They must all work together to complete the project. How could I explain to Hayden how long it would take Joseph working by himself?
----
Equation:
rate + rate + rate = together rate
1/8 + 1/6 + 1/x = together rate
---
Note: You did not post the together time. You need it
to solve for Joseph's time.
===============================
Cheers,
Stan H.
===============================
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! I did not see either your previous posting of the same problem, or the solution provided to you.
I could be saying the same thing all over again.
You would figure the rate at which each one works as
(work completed)/(time needed),
and you would figure out that rates add up,
because the rates mean how much work each one can do in an hour, and the amounts of work add up for each hour
(at least in math problems, where a worker can work as fast when starting work as when tired, after working for several hours).
The work rates for Cody and Kaitlin are known.
For Cody, the rate is
  .
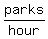For Kaitlin , the rate is
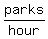
It it takes Joseph  hours to do the whole park by himself,
his rate would be  .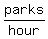
With the three of them working together, they may take  hours to do the park.
Their joint rate would be  ,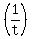
and we can conclude that
I can work with that equation to express it in other forms,
but with the data you have provided,
all I can get is } as a function of .,
or } as a function of .
It stands to reason that  ,
so  .
Beyond that, I cannot do anything else.
|
|
|
| |
