|
Question 817322: What is the equation of the hyperbola with vertices (0,4) and (0,-4) and asymptotic y=(1/3)x and y=(-1/3x)
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We plot the vertices and graph the asymptotes:
 The center of the hyberbola is (0,0) and it opens up and down since its
vertices are one above the other, so its equation is of the form
The center of the hyberbola is (0,0) and it opens up and down since its
vertices are one above the other, so its equation is of the form
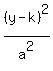  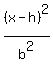   and since the center (h,k) is half-way between the vertices, the center
is the origin and (h,k) = (0,0) and therefore the equation of the hyperbola
is of the form
and since the center (h,k) is half-way between the vertices, the center
is the origin and (h,k) = (0,0) and therefore the equation of the hyperbola
is of the form
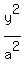  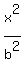   The top and bottom of the defining rectangle for the hyperbola will
be horizontal lines through the two vertices drawn between the two
asymptotes. These will be the horizontal lines y=4 and y=-4. So we
draw those two horizontal lines through the vertices:
The top and bottom of the defining rectangle for the hyperbola will
be horizontal lines through the two vertices drawn between the two
asymptotes. These will be the horizontal lines y=4 and y=-4. So we
draw those two horizontal lines through the vertices:
 Next we determine where those horizontal lines intersect the asymptotes
so that we can complete the defining rectangle:
We solve the system
Next we determine where those horizontal lines intersect the asymptotes
so that we can complete the defining rectangle:
We solve the system  by substitution by substitution
 12 = x
So the upper right corner of the defining rectangle is (12,4) and by
symmetry the other three corners are (-12,4),(-12,-4) and (12,-4).
So we draw in the sides of the defining rectangle, and sketch in the
hyperbola:
12 = x
So the upper right corner of the defining rectangle is (12,4) and by
symmetry the other three corners are (-12,4),(-12,-4) and (12,-4).
So we draw in the sides of the defining rectangle, and sketch in the
hyperbola:
 The transverse axis is the line between the two vertices, and the
semi-transverse axis is known as "a". so a=4 (the distance between the
center and either vertex.
The conjugate axis is the line through the center across the defining
rectangle, and the semi-conjugate axis is known as "b". so b=12
(the distance between the center and the middle of the side of the
defining rectangle. Therefore the equation of the hyperbola becomes:
The transverse axis is the line between the two vertices, and the
semi-transverse axis is known as "a". so a=4 (the distance between the
center and either vertex.
The conjugate axis is the line through the center across the defining
rectangle, and the semi-conjugate axis is known as "b". so b=12
(the distance between the center and the middle of the side of the
defining rectangle. Therefore the equation of the hyperbola becomes:
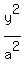  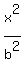  
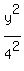    
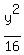     Clear of fractions by multiplying through by the LCD of 144
9y² - x² = 144
Edwin
Clear of fractions by multiplying through by the LCD of 144
9y² - x² = 144
Edwin
|
|
|
| |