SOLUTION: what is the standard form of the equation of a hyperbola with vertex (0,4) focus at (0,5) and center at (0,1)?

Hyperbolas have the equation 



if they look like this: )(

and the equation



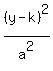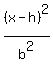if they look like this:

We plot the three given points for the vertex V, focus F 
and center C:



So it looks like this:

and has the equation



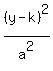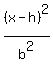We know that the center (h,k) is (0,1). We know that 
the semi-transverse axis, a, is the distance from the 
center to a vertex, and it is 3 units from C to V, so
a=3.  There is another vertex 3 units below the center
at (0,-2).

So we now have everything but b:



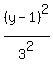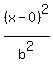We know that c is the distance from the center to a 
focus, and there are 4 units from C to F so c=4.  
There is another focus 4 units below the center at 
(0,-3).

In all hyperbolas we have the Pythagorean property

c² = a² + b²
4² = 3² + b²
16 = 9 + b²
 7 = b²
√7 = b

So now we know that b² = 7, a² =3² = 9, so the equation is:



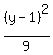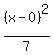or change (x-0)² to just x²



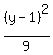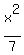Here is the complete graph.  The conjugate axis is the horizontal
line through the center, the width of the defining rectangle.
It is 2b units wide or 2√7, √7 on each side or about 2.7 on each 
side of the center.
  



Edwin