|
Question 746555: Determine the center, vertices, and foci for the following ellipse 18x^2+4y^2-108x+16y=106
Write word or phrase that best completes each statement or answers question
Found 2 solutions by MathLover1, KMST:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! An equation of the form
 represents an ellipse centered at (h,k), with an axis of length represents an ellipse centered at (h,k), with an axis of length  parallel to the x-axis, parallel to the x-axis,
and an axis of length 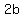 parallel to the y-axis. parallel to the y-axis.
If we can transform the equation given into such a form, we will be able to find everything the problem asks for.
 --> -->  --> -->  --> --> 
At this point, you look at the two expressions in brackets and have to realize that we can add something to each expression to "complete a square"
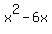 is part of is part of  and and
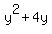 is part of is part of 
So  and and

So we go back to the original equation, and add  to both sides of the equal sign: to both sides of the equal sign:
 --> -->  --> -->  --> -->  --> --> 
Dividing both sides of the equal sign by 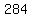 the equation turns into the equation turns into

That is the equation of an ellipse with  at (3,-2). at (3,-2).
The axis parallel to the y-axis (along  ) is longer, and it is called the major axis. ) is longer, and it is called the major axis.
Half of its length (called the semi-major axis) is

The 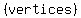 are the ends of the major axis, at a distance are the ends of the major axis, at a distance 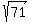 from the center, and are at from the center, and are at
( , , ) and ( ) and ( , ,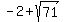 ) )
The other axis is called the minor axis.
It is along the line  , parallel to the x-axis. , parallel to the x-axis.
The ends of the minor axis (often called co-vertices) are at distance

That distance is called the semi-minor axis.
An ellipse has two  located on the major axis, between the center and the vertices, at a distance from the center located on the major axis, between the center and the vertices, at a distance from the center  called the focal distance. That distance called the focal distance. That distance  , and the semi-minor axis are the legs of a right triangle with the semi-major axis for a hypotenuse. , and the semi-minor axis are the legs of a right triangle with the semi-major axis for a hypotenuse.
Applying the Pythagorean theorem, we find that
 --> -->  --> -->  --> -->  --> -->  --> -->  --> --> 
So the  are at are at
( , , ) and ( ) and ( , ,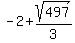 ) )
 
|
|
|
| |