SOLUTION: Ellipse Using Standard Form Vertices at (0,-1) and (12,-1), a focus at (6+√11-11).

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Ellipse Using Standard Form Vertices at (0,-1) and (12,-1), a focus at (6+√11-11).      Log On


   

Question 731952: Ellipse Using Standard Form
Vertices at (0,-1) and (12,-1), a focus at (6+√11-11).
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
The focus given is not clear. Either the "+" is a comma or the "-" is a comma. No matter, if those vertices are the main vertices, then a start on the form of the equation is like, %28x-6%29%5E2%2F36%2B%28y%2B1%29%5E2%2Fb%5E2=1, using center as half way between 0 and 12 on in reference to the x coordinate.

CONTINUING TO ANALYZE:
Assuming your given vertices are on the major axis and are horizontally arranged, the y coordinate of the foci MUST be in the exact same horizontal line as the major axis. y=-1 MUST contain the foci. If you tried to say that the coordinate pair for one of the foci is (6+11^(1/2), 11), then this is wrong. Saying that one of the foci were (6+11^(1/2), -1) would make sense. If this were one of the foci, then since both foci are equally distant from the center, and x=6 is one of the coordinates of the center, then the other focus must be (6-11^(1/2), -1).
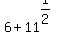The way that a, b, and c are related is a%5E2=b%5E2%2Bc%5E2. The value for c is 6%2B11%5E%281%2F2%29, which is the focal length. One simple algebra step gives b%5E2=a%5E2-c%5E2.

The equation for the ellipse can be amended as
%28x-6%29%5E2%2F36%2B%28y%2B1%29%5E2%2F%2836-%286%2B11%5E%280.5%29%29%5E2%29%5E2=1,
and you can finish the arithmetic in that.
[The algebra.com system is not rendering this last equation very neatly. Read it carefully.]