Question 699163: Find the coordinates of the center, the foci, and the vertices, and the equations and asymptotes of the graph of each equation. Then graph the equation.
x^2-4y^2-4x+24y-36=0
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
4x²-y²-8x+20 = 0 | x²-4y²-4x+24y-36 = 0
Rearrange the terms in this order x²,x,y²,y, and constants
on the right:
4x²-8x-y² = -20 x²-4x-4y²+24y = 36
4(x²-2x)-y² = -20 (x²-4x)-4(y²-6y) = 36
Complete the square in the parentheses. In the equation on
the left since there is no y-term write y as (y-0)
4(x²-2x+1)-(y-0)² = -20+4 (x²-4x+4)-4(y²-6y+9) = 36+4=36
4(x-1)²-(y-0)² = -16 (x-2)²-4(y-3)² = 4
Get 1 on the right by dividing through by the constant term:
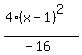  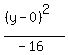   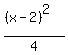  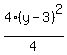  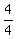
  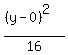   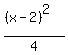  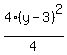  
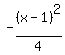  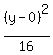   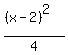  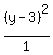   Switch the terms on the left so that the positive term comes first:
Switch the terms on the left so that the positive term comes first:
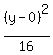  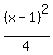   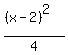  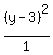   The equation on the left has its y-term first and therefore represents a
hyperbola that looks like this
The equation on the left has its y-term first and therefore represents a
hyperbola that looks like this  whereas the equation on the right
has its x-term first and therefore it represents a hyperbola that looks
like this )( whereas the equation on the right
has its x-term first and therefore it represents a hyperbola that looks
like this )(
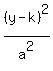  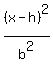   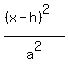    
  For the hyperbola on the left:
center=(h,k)=(1,0)
vertices=(h,k±a)=(1,4)&(1,-4)
focus=(h,k±c)
c²=a²+b²
c²=16+4
c²=20
c=√20
c=√4*5
c=2√5
focus=(h,k±c)=(1,±2√5)
asymptotes are the line through center (1,0)
with slope
For the hyperbola on the left:
center=(h,k)=(1,0)
vertices=(h,k±a)=(1,4)&(1,-4)
focus=(h,k±c)
c²=a²+b²
c²=16+4
c²=20
c=√20
c=√4*5
c=2√5
focus=(h,k±c)=(1,±2√5)
asymptotes are the line through center (1,0)
with slope 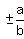 = = 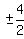 = ±2
Use point slope form.
They are y = 2x-2 and y = -2x+2
For the hyperbola on the right:
center=(h,k)=(2,3)
vertices=(h±a,k)=(4,3)&(0,3)
focus=(h±c,k)
c²=a²+b²
c²=4+1
c²=5
c=2√5
focus=(h±c,k)=(2±√5,3)
asymptotes are the line through center (2,3)
with slope = ±2
Use point slope form.
They are y = 2x-2 and y = -2x+2
For the hyperbola on the right:
center=(h,k)=(2,3)
vertices=(h±a,k)=(4,3)&(0,3)
focus=(h±c,k)
c²=a²+b²
c²=4+1
c²=5
c=2√5
focus=(h±c,k)=(2±√5,3)
asymptotes are the line through center (2,3)
with slope  = =  Use point slope form.
They are y =
Use point slope form.
They are y =  x+2 and y = x+2 and y =  x+4
Edwin x+4
Edwin
|
|
|