Question 668472: it says, "Identify the curve and find the characteristics listed. then sketch the curve."
(x-3)^2/9 - (y+5)^2/16=1 center, asymptotes, vertices, foci
(y-2)^2 = (x-3) center, directrix, focus
Answer by lwsshak3(11628)   (Show Source):
You can put this solution on YOUR website! "Identify the curve and find the characteristics listed. then sketch the curve."
(x-3)^2/9 - (y+5)^2/16=1 center, asymptotes, vertices, foci
(x-3)^2/9-(y+5)^2/16=1
This is an equation of a hyperbola with horizontal transverse axis.
Its standard form: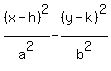 =1, (h,k)=(x,y) coordinates of center
For given equation:
center: (3,-5)
a^2=9
a=√9=3
vertices=(3±a,-5)=(3±3,-5)=(6,-5) and (0,-5)
..
b^2=16
b=√16=4
Foci:
c^2=a^2+b^2=9+16=25
c=√25=5
Foci=(3±c,5)=(3±5,5)=(8,5) and (-2,5)
..
asymptotes are straight lines that go thru the center and are of the form: y=mx+b, m=slope, b=y-intercept
slopes of asymptotes for hyperbolas with horizontal transverse axis=±b/a=±4/3
Equations of asymptotes:
y=4x/3+b
solve for b using coordinates of center
-5=4*3/3+b
b=-9
equation:y=4x/3-9
and
y=-4x/3+b
-5=-4*3/3+b
b=-1
equation:y=-4x/3-1
..
see graph below:
y=((16(x-3)^2/9)-16)^.5-5
..
(y-2)^2 = (x-3) center, directrix, focus
This is an equation of a parabola that opens rightwards:
Its standard form: (y-k)^2=4p(x-h), (h,k) =(x,y) coordinates of the vertex (not center)
For given equation: (y-2)^2=(x-3)
vertex: (3,2)
axis of symmetry: y=2
4p=1
p=1/4
focus: (3+1/4,2)=(13/4,2) (p-distance from vertex on the axis of symmetry)
directrix: x=3-1/4=11/4 (vertical line p-distance from vertex on the axis of symmetry
se graph below:
y=±(x-3)^.5+2
|
|
|
