Hi,
transverse axis for hyperbola:
C(0,0) Vertices (0,±
)
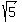Opens Up and Down along x = 0 or the y-axis. tranverse axis is the y-axis.
See below descriptions of various conics
Standard Form of an Equation of a Circle is 
where Pt(h,k) is the center and r is the radius
Standard Form of an Equation of an Ellipse is 
where Pt(h,k) is the center. (a positioned to correspond with major axis)
a and b are the respective vertices distances from center
and ±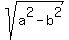
are the foci distances from center: a > b
Standard Form of an Equation of an Hyperbola opening right and left is:
where Pt(h,k) is a center with vertices 'a' units right and left of center
and foci 
units right and left of center along y = k
Standard Form of an Equation of an Hyperbola opening up and down is:
where Pt(h,k) is a center with vertices 'b' units up and down from center,
and foci units units up and down from center, along x = h
the vertex form of a Parabola opening up(a>0) or down(a<0), 
where(h,k) is the vertex.
The standard form is 
, where the focus is (h,k + p)
the vertex form of a Parabola opening right(a>0) or left(a<0), 
where(h,k) is the vertex.
The standard form is 
, where the focus is (h +p,k )
