|
Question 619252: Whats the standard form of an ellipse with verticies at (-5,-6) and (-5,8) and a minor axis of 6?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! STEP 1 - FIND THE DIRECTION OF THE MAJOR AXIS:
The major axis extends between the vertices, and since the vertices have the same x-coordinate (x=-5), the major axis is vertical (parallel to the y-axis), along the line x=-5.
On that line, we find the vertices, the foci, and the center.
STEP 2 - FIND THE CENTER:
The center is midway between the vertices, so we average the coordinates of the vertices to find the midpoint of the segment (the major axis) that connects those vertices.
We already know that the x-coordinate is -5.
We just need to average the y-coordinates of the vertices.
The center will be (-5, )=(-5,1)
STEP 3 - FIND THE SEMI-MAJOR AXIS:
The semi-major axis is called a, and is the distance from the center to a vertex.
It's 
(It could also be calculated as half the distance between the vertices).
STEP 4 - FIND THE SEMI-MINOR AXIS:
The minor axis is the distance between the co-vertices, and the problem says it's 6.
The semi-minor axis is called b, and is half of the minor axis, so b=3.
STEP 5 - WRITE THE EQUATION:
The equation involves the coordinates of the center (x=-5, y=1), subtracted from x and y, and then squared:
 and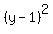 
Those squares are divided by  and  .
Since the major axis extends vertically, the  will be dividing the .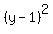
The equation is
 or 
It shows that from the center (-5,1), the ellipse extends horizontally 3 units to the left and to the right, to co-vertices with y=1, such that
 or  or  , and
that it extends vertically 7 units up and down from the center to vertices with x=-5, and such that
 or 
|
|
|
| |
