|
Question 619024: Identify the vertices, co-vertices and foci of the ellipse for each equation
a. x^2/36 + y^2/16 =1
b. (x+5)^2 + y^2/49 = 1
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll do one (the second one because it it a little harder). And you can use that to figure out the other one.

First we must recognize that this the the equation of an ellipse. If you were to multiply out the left side you would find that there is both an x squared and a y squared term (and no xy terms) and that the coefficients of these squared terms are unequal and both positive. This is what makes the equation an ellipse.
The standard form of the equation of an ellipse is:
 for horizontal ellipses, and for horizontal ellipses, and
 for vertical ellipses for vertical ellipses
In these equations, the "h" and the "k" are the x and y coordinates, respectively, of the center. The "a" is the distance from the center to each vertex and the "b" is the distance from the center to each co-vertex. Since the vertices are farther away from the center than the co-vertices, a > b. (This is important to know because that is how you determine which denominator is  and which is and which is  ). ).
So let's put our equation in standard form. We need a denominator under the  . As I'm sure you've done many times before, you can make a fraction out of something by putting it over a 1: . As I'm sure you've done many times before, you can make a fraction out of something by putting it over a 1:

Next we want denominators that are perfect squares. Since  and and  : :

(Note: If oone of the denominators had not been a perfect square, we could still work with it. For example, if the 49 had been 59, then we could rewrite the denominator as 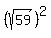 The rest of the problem would be a little harder because our "a" is a square root, but we could still finish the problem.) The rest of the problem would be a little harder because our "a" is a square root, but we could still finish the problem.)
Next we want each numerators to be the square of of a subtraction. With a little thought I hope you can see that  and that and that  : :

We now have the equation in standard form. From thsi we can "read":
h = -2 and k = 0 making the center: (-2, 0)
a = 7 (Remember a > b! So the a can't be the 1)
b = 1
And since the  is found under the "y-term", this is the equation for a vertical ellipse. (This is important because it tells us that the vertices (and foci) will be above and below the center (not to the right and left of it) and the co-vertices will be right and left of the center. is found under the "y-term", this is the equation for a vertical ellipse. (This is important because it tells us that the vertices (and foci) will be above and below the center (not to the right and left of it) and the co-vertices will be right and left of the center.
So the vertices will be "a" distance above and below the center. To go up and down we change the y coordinate so:
Vertices: (-2, 0+7) or (-2, 7) and
(-2, 0-7) or (-2, -7)
The co-vertices are right and left and to go this direction we change the x coordinates:
Co-vertices: (-2+1, 0) or (-1, 0) and
(-2-1, 0) or (-3, 0)
Last of all we need the foci. The distance from the center to each focus is called "c". The "c" is not in the standard form of the equation for an ellipse. But there is a fixed relationship between the "a", the "b" and the "c" values:

(Note: There is a very similar but different equation connecting the "a", "b" and "c" values for hyperbolas"  . A way to remmeber which of these to use is to remember that the foci for an ellipse are inside the ellipse. So a > c in ellipses. For hyperbolas, the foci are farther away from the center than the vertices. So c > a for hyperbolas. The equations illustrate these facts. The largest value, "a" or "c", is the one that is by itself in the equation.) . A way to remmeber which of these to use is to remember that the foci for an ellipse are inside the ellipse. So a > c in ellipses. For hyperbolas, the foci are farther away from the center than the vertices. So c > a for hyperbolas. The equations illustrate these facts. The largest value, "a" or "c", is the one that is by itself in the equation.)
So we use  to find "c", using the values we have for "a" and "b": to find "c", using the values we have for "a" and "b":




The foci, like the vertices, will be up and down from the center of a vertical ellipse. So:
Foci: (-2, 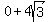 ) or (-2, ) or (-2, 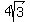 ) and
(-2, ) and
(-2, 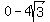 ) or (-2, ) or (-2, 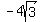 ) )
|
|
|
| |