Question 612542: find the equation of the ellipse with the following properties.
x-intercepts (5,0) and (-5,0); y-intercepts (0,3) and (0,-3)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form for the equation of an ellipse is

Since the intercepts are on the ellipse in question, they must fit the equation. Substituting (5, 0) into this equation we get:

which simplifies to:

Subtracting 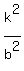 from each side: from each side:

Multiplying by  : :

Substituting (-5, 0) into  and following the same steps as above we end up with: and following the same steps as above we end up with:

Since 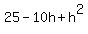 and and 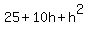 are both equal to are both equal to  , they must be equal to each other: , they must be equal to each other:

We can solve this for h. Subtracting 25 and  and adding 10h we get: and adding 10h we get:
0 = 20h
Dividing by 20:
0 = h
Using (0, 3) and (0, -3) and logic just like the above we can find that k = 0.
This makes the center of the ellipse (0, 0).
Since the center, (5, 0) and (-5, 0) are all on the x-axis, the given points are not just the intercepts, they are the vertices on the major axis of the ellipse. This means the "a" is 5.
Since the center, (0, 3) and (-5, 0) are all on the y-axis, the given points are not just the intercepts, they are the vertices on the minor axis of the ellipse. This means the "b" is 3.
With the center, a and b we can now write the equation:

which simplifies to:

|
|
|