|
Question 612377: Major axis 16 units long, center at (0,0), foci at (0, 2√15) and (0,-2√15)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume the problem is to find the equation of the conic section being described. In the future, please include the directions for problem.
With a major axis and two foci we are dealing with either an ellipse or a hyperbola.
Since the major axis is 16 units long, "a" must be 8.
Since the foci are (0, 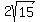 ) and (0, ) and (0, 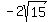 ) and since the center of an ellipse or hyperbola is always half way between the foci, the center must be at (0, 0) ) and since the center of an ellipse or hyperbola is always half way between the foci, the center must be at (0, 0)
With foci of (0, 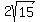 ) and (0, ) and (0, 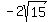 ) and with a center of (0, 0), the "c" must be ) and with a center of (0, 0), the "c" must be 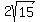
Since 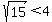 , , 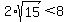 . So c < 8. And since c < a we must be dealing with an ellipse. . So c < 8. And since c < a we must be dealing with an ellipse.
Since the foci are up and down from each other (the x's are the same but the y's are different), the major axis of the ellipse is vertical.
The only piece of information we still need is the "b". The relationship between a, b and c in an ellipse is:

Substituting in our values for a and c we get:

Simplifying:


Subtracting 60:

2 = b (We can ignore the fact that b could also be -2 since b must be positive.)
The standard form for the equation of a vertically-oriented ellipse is:

with "h" being the x coordinate of the center and "k" being the y coordinate of the center. Substituting in our center and "a" and "b" we get:

which simplifies to:

|
|
|
| |