|
Question 610731: In an equilateral triangle with one vertex at the origin
and one with coordinates
(8,0) find the possible coordinates
of the third vertex
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since one vertex and another is at (8, 0) it follows that the length of that side is 8. And since all the sides of an equilateral triangle are congruent, the other two sides also have a length of 8.
If we call the origin A and (8,0) B and the missing vertex C, then we are looking for the coordinates of C that makes its distance from A and from B equal to 8. If you draw a diagram it might help. In addition to points A and B, draw two circles with a radius of 8. One circle should have A as the center and the other will have will have B as the center. The first circle represents all the points that are 8 away from A and the second circle represents all the points that are 8 away from B. The points where they intersect, one in the 1st quadrant and one in the second quadrant, represent the only points that are 8 away from both A and B. These points are the C's that we are looking for.
From each possible C, draw a perpendicular to the x-axis. This forms right triangles. The hypotenuses of these triangles are 8's. And the legs represent the x and y coordinates of the point C. And the angle between the x-axis and the hypotenuse's are 60's since the angles in every equilateral triangle are always 60 degrees. This makes our right triangles 30-60-90 right triangles.
If we remember the pattern for these triangles we know that the hypotenuse is always twice as big as the side opposite the 30 degree angle. In other words the side opposite the 30 degree angle is half the hypotenuse. So the side opposite the 30 degree angle, on the x-axis, is going to be half of 8 which is 4.
The other part of the pattern for these triangles is that the side opposite the 60 degree angle is always  times the side opposite the 30 degree angle. So the side opposite the 60 degree angle, the vertical leg, will be times the side opposite the 30 degree angle. So the side opposite the 60 degree angle, the vertical leg, will be 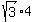 or or 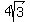 . .
Now we have the information we need for the coordinates of the possible 3rd vertices:
In the first quadrant: (4, 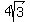 ) )
In the fourth quadrant: (4, 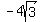 ) )
|
|
|
| |