SOLUTION: Find the equation of the hyperbola whose vertices are at (-1,-5) and (-1,1) with a focus at (-1,-7). Please show me how to do this. Thank you and God bless.

We plot the two vertices (-1,1) and (-1,-5), and draw the transverse
axis, "trans-" means "across" and "-verse" means "vertices".



The equation of a hyperbola with a vertical transverse axis is

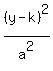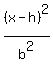 -  = 1

The transverse axis is 6 units long, and the value of "a" is the
length of the semi-transverse axis, which is half of 6 which is 3.
So not we have 

a = 3

The center is the midpoint between the two vertices,

which is the point (h,k) = (-1,-2),  So we plot that point:



Next we plot the given focus (-1,7):



The distance known as "c" is the distance from the focus to the center.
We count tho units and find that it is 5 units fron the center (-1,-2)
to the focus (-1,-7).  Therefore c = 5

All hyperbolas have this Pythagorean theorem relationship:
Substituting a=3 and c=5 

c² = a² + b²
5² = 3² + b²
25 = 9 + b²
16 = b²
 4 = b

Now we have the equation sice we know a = 3, b = 4, (h,k) = (-1,-2)

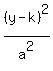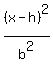 -  = 1
becomes:

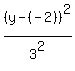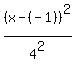 -  = 1

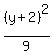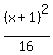 -  = 1

That's the answer, but let's finish drawing the graph:

Draw the conjugate axis, which is a horizontal line 2b
or 2(4) = 8 units long with the center as its midpoint:



Next we draw the defining rectangle, which is a rectangle with
horizontal and vertical sides with the ends of the transverse and
conjugate axes as their midpoints:

 

Draw and extend the diagonals of the defining rectangle:

 

And finally sketch in the hyperbola with the given vertices and
approaching the diagonals:

  

If you were asked to find the equations of the asymptotes it would
not be difficult since you have points that each one goes through,
the center and corner points of the defining rectangle.

Edwin