|
Question 572756: Give the equation in standard form of the hyperbola with vertices (-4,2)
and (1,2) and foci (-7,2) and (4,2). Give the center and the asymptotes.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Give the equation in standard form of the hyperbola with vertices (-4,2)
and (1,2) and foci (-7,2) and (4,2). Give the center and the asymptotes.
In a message dated 6/24/2011 2:53:25 P.M. Eastern Daylight Time, AnlytcPhil@aol.com writes:
what is the equation of a hyperbola with vertices (-5,3) (-1,3) and foci (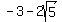 , 3) and ( , 3) and (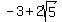 , 3)
First we plot the vertices: , 3)
First we plot the vertices:
 We see that the hyperbola opens right and left, that is,
it looks something like this: )(
So we know its standard equation is this:
We see that the hyperbola opens right and left, that is,
it looks something like this: )(
So we know its standard equation is this:
 We connect the vertices to find the transverse axis:
We connect the vertices to find the transverse axis:
 We can see that the transverse axis is 5 units long, and since the
transverse axis is 2a units long, then 2a=5 and a=
We can see that the transverse axis is 5 units long, and since the
transverse axis is 2a units long, then 2a=5 and a= The center of the hyperbola is the midpoint of the transverse axis,
and we can see that the midpoint of the transverse axis is (
The center of the hyperbola is the midpoint of the transverse axis,
and we can see that the midpoint of the transverse axis is ( ,2), so
we have (h,k) = ( ,2), so
we have (h,k) = ( ,2). So we plot the center: ,2). So we plot the center:
 To find a, we subtract the x-coordinate of
the center from the x-coordinate of the right vertex, and get
1 - (
To find a, we subtract the x-coordinate of
the center from the x-coordinate of the right vertex, and get
1 - ( ) = ) = 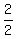 + +  = =  So a=
So a= .
We are given the foci (-7,2) and (4,2)
The number of units from each of the foci to the center is the value c.
To find that distance c, we subtract the x-coordinate of the center
from the x-coordinate of the right focus, and get
c = 4 - ( .
We are given the foci (-7,2) and (4,2)
The number of units from each of the foci to the center is the value c.
To find that distance c, we subtract the x-coordinate of the center
from the x-coordinate of the right focus, and get
c = 4 - (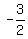 = = 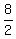 + +  = =  Next we find b from the Pythagorean relationship common to all
hyperbolas, which is
c² = a² + b²
Substituting for c and a
Next we find b from the Pythagorean relationship common to all
hyperbolas, which is
c² = a² + b²
Substituting for c and a
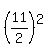 = ( = ( )² + b² )² + b²
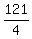 = =  + b² + b²
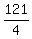 - -  = b² = b²
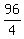 = b²
24 = b² = b²
24 = b²
 = b = b
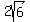 = b
Now we can give the standard equation of the hyperbola, since we now
know h, k, a, and b, a² and b²: = b
Now we can give the standard equation of the hyperbola, since we now
know h, k, a, and b, a² and b²:
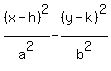 = 1 = 1
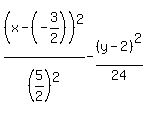 = 1 = 1
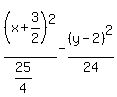 = 1
Next we draw in the conjugate axis which is 2b units
or = 1
Next we draw in the conjugate axis which is 2b units
or  or about 4.9 units long with the center as its midpoint.
That is, we draw a vertical line or about 4.9 units long with the center as its midpoint.
That is, we draw a vertical line  , about 2.45 units
upward and the same number of units downward from the center: , about 2.45 units
upward and the same number of units downward from the center:
 Next we draw the defining 2a×2b rectangle which has the transverse axis
and the conjugate axis as perpendicular bisectors of its sides:
Next we draw the defining 2a×2b rectangle which has the transverse axis
and the conjugate axis as perpendicular bisectors of its sides:
 Next we draw the extended diagonals of the defining rectangle:
Next we draw the extended diagonals of the defining rectangle:
 We can now sketch in the hyperbola:
We can now sketch in the hyperbola:
 But we still have to find the equations of those two blue
asymptotes.
We know one point they go through, namely the center (
But we still have to find the equations of those two blue
asymptotes.
We know one point they go through, namely the center ( ,2)
We need to know the slopes of the two asymptotes. They are ,2)
We need to know the slopes of the two asymptotes. They are
 = ± = ± = ± = ± = ± = ±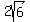 · · = ± = ±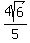 Now we use the point-slope form.
y - y1 = m(x - x1)
y - 2 = ±
Now we use the point-slope form.
y - y1 = m(x - x1)
y - 2 = ±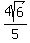 (x - ( (x - ( ))
y - 2 = ± ))
y - 2 = ±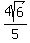 (x + (x +  )
y = 2 ± )
y = 2 ± 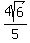 (x + (x +  )
One asymptote has the equation with the positive slope,
and the other has the equation with the negative slope.
Edwin )
One asymptote has the equation with the positive slope,
and the other has the equation with the negative slope.
Edwin
|
|
|
| |