SOLUTION: find the equation of the ellipse satisfying the given conditions: canter at (0,0); foci at (0,4) and (0,-4); vertices at (0,7) and (0,-7); and major axis along the y-axis

It has equation  

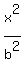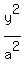 +  = 1

and a = 7, so we have a² = 49

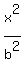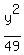 +  = 1

Here are a bunch of ellipses with center (0,0) and vertices at (0,7) and (0,-7).



To find out which it is, we must calculate "b", the semi-minor axis:

The relationship between a, b, and c in all ellipses is

c² = a² - b²

where c is the distance from the center to either focus.

The foci are (0,±4) and the vertices are (0,±7)

So c = 3

c² = a² - b²
   
4² = 7² - b²

16 = 49 - b²

-33 = -b²

 33 = b²

 = b

So the equation is:

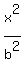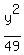 +  = 1

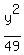 +  = 1

And the graph is:

 


Edwin