I am a freshman in honors algebra 2 and we're working on applying prabolas to real world senarios. The question is " find the dimensions and maximum area of a rectangle with a perimeter of 48 inches" all I have now is basic rectangle properties because I spaced off in class. Please help me.
A = L×W where A = area, L = length and W = wifth
P = 2L + 2W where P = perimeter
Let the length be x
Since the perimeter is 48, we substitute in
P = 2L + 2W
48 = 2x + 2W
Divide every term by 2
24 = x + W
Solve for W
24 - x = W
Let the area be y. Substitute in
A = L×W
y = x(24 - x)
That equation has this graph:
 Since y = the area, the area will be a maximum at the
peak point, known as "the vertex".
There are three ways to find the vertex. I don't know which way
your teacher will require you to use.
Method 1 for finding the vertex:
Find the two x-intercepts
y = x(24 - x)
x(24 - x) = 0
x=0, 24-x = 0
-x = -24
x = 24
The x-intercepts are (0,0) and (24,0)
The vertex occurs halfway when the value of x is halfway
between 0 and 24, or at x=12.
Substituting x=12
y = 12(24-12)
y = 12(12)
y = 144
So the vertex of that parabola is (12,144)
That means the area y will have a maximium area of 144 square units
when the length is x = 12 inches. That is, when the rectangle is a
12in × 12in square.
-----------------------------------------
Method 2 for finding the vertex:
y = x(24 - x)
Put the equation in the vertex form:
y = a(x-h)² + k
y = x(24 - x)
y = 24x - x²
y = -x² + 24x
Factor out the coefficient of x², which is -1
y = -1[x² - 24x ]
Complete the square by multiplying the coefficient of x by
Since y = the area, the area will be a maximum at the
peak point, known as "the vertex".
There are three ways to find the vertex. I don't know which way
your teacher will require you to use.
Method 1 for finding the vertex:
Find the two x-intercepts
y = x(24 - x)
x(24 - x) = 0
x=0, 24-x = 0
-x = -24
x = 24
The x-intercepts are (0,0) and (24,0)
The vertex occurs halfway when the value of x is halfway
between 0 and 24, or at x=12.
Substituting x=12
y = 12(24-12)
y = 12(12)
y = 144
So the vertex of that parabola is (12,144)
That means the area y will have a maximium area of 144 square units
when the length is x = 12 inches. That is, when the rectangle is a
12in × 12in square.
-----------------------------------------
Method 2 for finding the vertex:
y = x(24 - x)
Put the equation in the vertex form:
y = a(x-h)² + k
y = x(24 - x)
y = 24x - x²
y = -x² + 24x
Factor out the coefficient of x², which is -1
y = -1[x² - 24x ]
Complete the square by multiplying the coefficient of x by  ans squaring: -24(
ans squaring: -24( ) = -12, Squaring (-12)² = 144
Add and subtract 144 inside the parentheses:
y = -1[x² - 24x + 144 - 144]
Factor the first three terms in the brackets as the square of a
binomial
y = -1[(x - 12)² - 144]
Remove the bracket leving the paretheses intact:
y = -1(x - 12)² + 144
Compare to
y = a(x-h)² + k
Vertex = (h,k) = (12,144)
-------------------------------------
Method 3 for finding the vertex:
Use the vertex formula:
The vertex is (h,k) where
h =
) = -12, Squaring (-12)² = 144
Add and subtract 144 inside the parentheses:
y = -1[x² - 24x + 144 - 144]
Factor the first three terms in the brackets as the square of a
binomial
y = -1[(x - 12)² - 144]
Remove the bracket leving the paretheses intact:
y = -1(x - 12)² + 144
Compare to
y = a(x-h)² + k
Vertex = (h,k) = (12,144)
-------------------------------------
Method 3 for finding the vertex:
Use the vertex formula:
The vertex is (h,k) where
h = 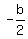 and k =
and k =  y = -x² + 24x
y = -x² + 24x + 0
a = -1, b = 24, c = 0
h =
y = -x² + 24x
y = -x² + 24x + 0
a = -1, b = 24, c = 0
h = 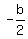 and k =
and k =  h =
h = 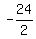 = -12
k =
= -12
k =  k = -1(12)^2+24(12)+0
k = -(144)+ 288
k = 144
So the vertex is (12,144)
Use whichever method for finding the vertex your teacher
expects you to use, not necessarily the easiest way.
Edwin
k = -1(12)^2+24(12)+0
k = -(144)+ 288
k = 144
So the vertex is (12,144)
Use whichever method for finding the vertex your teacher
expects you to use, not necessarily the easiest way.
Edwin