SOLUTION: Find an equation of the ellipse centered at (0,0), with a vertex at (9,0) and asymptote y=1/4x

Ellipses do not have asymptotes.  Hyperbolas do.  Did you mean 
"hyperbola" and typed "ellipse" instead?  I will assume that's
what you did.

Since one asymptote is y = x, the othe one is y = x.

We draw those, plot the vertices (9,0) and (-9,0), and and sketch the hyperbola to approach them.



Then we draw in the defining rectangle:

  

By letting x=4 and -4 in each of those asymptote equations we can 
see that the corners of the defining rectangle are:

(9,), (9,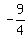), (-9,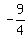), and (-9,)

so a = 9 and b = , so the equation is

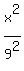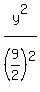 -  = 1

Edwin