We have to get it either in the form:
+ 
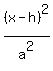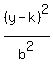= 1
in which the ellipse will look like this "
"
or this form:
+ 
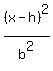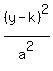= 1
in which the ellipse will look like this "
"
9x² + 4y² - 54x + 16y + 61 = 0
Get the x terms together, and the y terms together.
9x² - 54x + 4y² + 16y + 61 = 0
Get the 61 off the left side by adding -61 to both sides
9x² - 54x + 4y² + 16y = -61
Factor the 9 out of the first two terms on the left
(factor out just the 9, not the x)
9(x² - 6x) + 4y² + 16y = -61
Factor the 4 out of the last two terms on the left
(factor out just the 4, not the y)
9(x² - 6x) + 4(y² + 4y) = -61
Complete the square inside the first parentheses:
Multiply the coefficient of x, which is -6 by 
, getting -3
Square -3 getting (-3)² = 9
Add 9 inside at the end of the first parentheses:
9(x² - 6x + 9) + 4(y² + 4y) = -61 + 81
Notice that to offset adding the 9 inside the parentheses,
we had to add 81 to the right side. That's because when
we added 9 inside the first parentheses on the left, that
actually amounted to adding 9·9 or 81 to the left side
because of the 9 coefficient in front of the first parentheses
on the left.
Complete the square inside the second parentheses:
Multiply the coefficient of y, which is 4 by , getting 2
Square 2 getting (2)² = 4
Add 4 inside at the end of the second parentheses:
9(x² - 6x + 9) + 4(y² + 4y + 4) = -61 + 81 + 16
Notice that to offset adding the 4 inside the parentheses,
we had to add 16 to the right side. That's because when
we added 4 inside the second parentheses on the left, that
actually amounted to adding 4·4 or 16 to the left side
because of the 4 coefficient in front of the second parentheses
on the left.
Next we factor the two parentheses and combine the terms on the
right:
9(x - 3)(x - 3) + 4(y + 2)(y + 2) = 36
Those factorizations can be written shorter as the squares of
binomials:
9(x - 3)² + 4(y + 2)² = 36
In fact most people skip the step before the last one.
Next we must get a 1 on the right side. So we divide each
term by 36:
+ 
= 
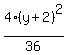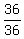We simplify:
+ 
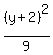= 1
Now we compare that to
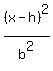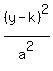+ = 1
and the ellipse will look like this ""
We can tell that because a² is larger than b².
On comparing the two we see that h=3, k=-2, b²=4 or b=2, a²=9, or a=3
The center is (h,k) = (3,-2).
We plot the center (3,-2)
We draw the major axis vertically, which is bisected at the center.
We count a=3 units up from the center and a=3 units down from the
center to the vertices. The vertex which is 3 units above the center
(3,-2) is the point (3,1). The vertex which is 3 units down from
the center is the point (3,-5):
We draw the minor axis vertically, which is also bisected at the center.
We count b=2 units left from the center and b=2 units right from the
center to the covertices. The covertex which is 2 units left of the center
(3,-2) is the point (1,-2). The covertex which is 2 units right of
the center is the point (5,-2):
Now we can sketch in the ellipse:
All we need to do now is to find the foci. They are two points inside
the ellipse on the major axis each of which is "c" units from the center,
where c is calculated from this Pythagorean relation:
c² = a² - b²
c² = 9 - 4
c² = 5
c = 
.
To find the coordinates of the upper focus, we add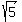 
to the
y coordinate of the center and get the point (3,-2+). To
get the lower focus, we subtract from the y coordinate of the
center and get the point (3,-2-).
We plot them:
Center: (3,-2), Vertices: (3,1) and (3,-5), Covertices: (1,-2) and (5,-2)
Foci: (3,-2-) and (3,-2+), Major axis: 2a = 6,
Minor axis: 2b = 4. Eccentricity: 
= 
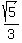Edwin
