|
Question 552371: What is the axis of symmetry of y=7(x+1)(x-3) I have tried another website and it stated something about h=x, and h would be the 1 in the first set of parenthesis, correct? Or is there some other method that is more accurate? Thank you.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's a graph of your equation.
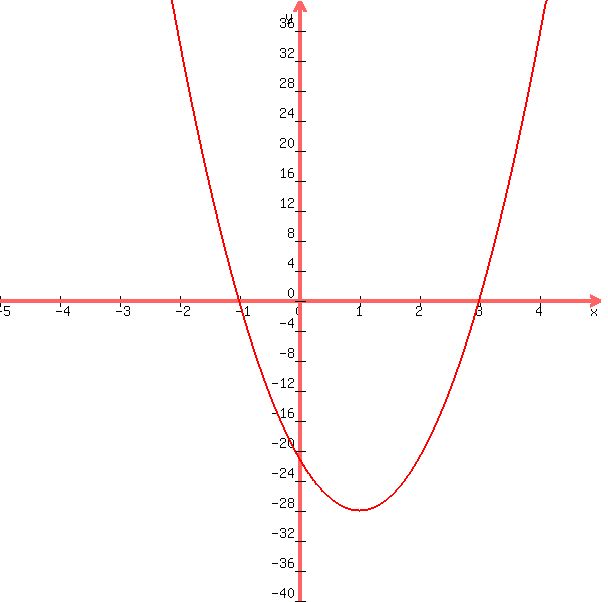
the axis of symmetry would be at x = 1 because the graph y = 0 at x = -1 and x = 3 and the axis of symmetry would be halfway between them.
this is not, however, how you would find the axis of symmetry in general.
what you have is a quadratic equation whose roots are x = -1 and x = 3.
those roots are the places where the equation crosses the x-axis.
if the equation had no roots, you would not be able to find the axis of symmetry that way.
the other way is to place the equation in quadratic form and then use the formula for the axis of symmetry, which is:
x = -b/2a
to place the equation in quadratic form, multiply out the factors to get:
7(x+1)(x-3) = 7x^2 - 14x - 21
a is the coefficient of the x^2 term which equals 7
b is the coefficient of the x term which equals -14
c is the constant term.
the axis of symmetry is given by using the formula of:
x = -b/2a and replacing b with -14 and a with 7 to get:
x = -(-14)/14 = -1.
this confirms what you were able to see on the graph.
to find the roots of this equation, you would do the following:
the equation is 7x^2 - 14x - 21
set it equal to 0 to get:
7x^2 - 14x - 21 = 0
divide both sides of the equation by 7 to get:
x^2 - 2x - 3 = 0
factor it to get:
(x-3)(x+1) = 0
set each of these factors equal to 0 and solve for x to get:
x = 3
x = -1
those are the roots.
they are real.
the graph of the equation crosses the x-axis at those points.
the axis of symmetry is halfway between them at x = 1
draw a vertical line at x = 1 and it cuts the graph into 2 symmetrical halves.
Answer by ikleyn(53299)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the axis of symmetry of y=7(x+1)(x-3) I have tried another website and it stated
something about h=x, and h would be the 1 in the first set of parenthesis, correct?
Or is there some other method that is more accurate? Thank you.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
32 lines in the post by @Theo is a complete waste of time.
True solution is very simple and very short.
The given polynomial describes a parabola opened up.
This polynomial has two roots at x = -1 and x = 3 (look at the factors in parentheses).
It means that the parabola intersects x-axis in points x = -1 and x=3.
The axis of symmetry of this parabola is vertical line and it is half-way between the roots.
Midpoint between the roots is x =  = = 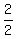 = 1. = 1.
Therefore, equation of the symmetry line of this parabola is x = 1.
It is how this problem should be solved and how the solution should be presented.
It is a standard mantra to pronounce when solving this problem.
It is what your teacher wants to hear from you.
|
|
|
| |