|
Question 481497: Find the focus and directrix of each parabola with the given equation.
a). x^=4y
b). y^=-4x
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the focus and directrix of each parabola with the given equation.
a). x^=4y
b). y^=-4x
**
a). x^2=4y
This is an equation of a parabola with a vertical axis of symmetry.
Its standard form: (x-h)^2=4p(y-k), with (h,k) being the (x,y) coordinates of the vertex.
For given equation:
parabola opens upwards
Vertex(0,0)
4p=4
p=1
Focus:(0,1)
Directrix: y=-1
see the graph below as a visual check on the answers:
..
y=±x^2/4
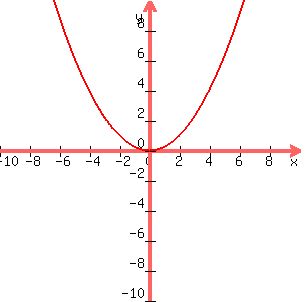
..
b). y^2=-4x
This is an equation of a parabola with a horizontal axis of symmetry.
Its standard form: (y-k)^2=4p(x-h), with (h,k) being the (x,y) coordinates of the vertex.
For given equation:
parabola opens leftward
Vertex(0,0)
4p=4
p=1
Focus:(-1,0)
Directrix: x=1
see the graph below as a visual check on the answers:
..
y=±(-4x)^.5

..
|
|
|
| |