|
Question 480300: find the ellipse in standard form that passes through the
point(3,sqrt(7)) and (sqrt(3),3)?
Found 2 solutions by Edwin McCravy, Alan3354:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! point(3, ) and ( ) and ( ,3)? ,3)?
Here are those two points plotted: approximately (3,2.6) and (1.7,3)
 I will assume you meant the ellipse with center at the origin;
otherwise there would be many possibilities.
Since those points are as they are, the major axis will be
horizontal and the ellipse will look like this: ᆼ
So its equation will be:
I will assume you meant the ellipse with center at the origin;
otherwise there would be many possibilities.
Since those points are as they are, the major axis will be
horizontal and the ellipse will look like this: ᆼ
So its equation will be:
 Substitute the first point: (x, y) = (3,
Substitute the first point: (x, y) = (3,  ) )

 Substitute the second point: (x, y) = (
Substitute the second point: (x, y) = ( ,3)? ,3)?

 We have this system of equations:
We have this system of equations:
 Important!:
DO NOT CLEAR OF FRACTIONS BUT SOLVE BY ELIMINATION:
Multiply the 2nd equation through by -3 to eliminate the
terms in aČ:
Important!:
DO NOT CLEAR OF FRACTIONS BUT SOLVE BY ELIMINATION:
Multiply the 2nd equation through by -3 to eliminate the
terms in aČ:
 Add the equations:
Add the equations:


 Substitute 10 for bČ in the first equation:
Substitute 10 for bČ in the first equation:

 Multiply through by 10aČ
Multiply through by 10aČ


 Substitute 30 for aČ and 10 for bČ
Substitute 30 for aČ and 10 for bČ

 That's the equation.
The vertices are (±
That's the equation.
The vertices are (±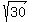 ,0), approximately (±5.5,0)
The covertices are (0,± ,0), approximately (±5.5,0)
The covertices are (0,± ), approximately (0,±3.2)
Here's the graph: ), approximately (0,±3.2)
Here's the graph:
 Edwin
Edwin
Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|
| |