|
Question 471933: Find an equation of the ellipse having the given points as foci and the given sum of the focal radii
(-9, 0); (9, 0); 30
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an equation of the ellipse having the given points as foci and the given sum of the focal radii
(-9, 0); (9, 0); 30
**
I could not fine anywhere the definition of "focal radii". I think you meant it to be the constant sum of the distances from any point of the ellipse to each focus. I will assume this is the intended definition which is equal to the major axis.
..
From given coordinates of the Foci, it can be seen that the equation has a horizontal major axis.(x changes but y does not) Standard form of ellipse for this equation: (x-h)^2/a^2+(y-k)^2/b^2=1, (a>b), with (h,k) being the (x,y) coordinates of the center.
..
center: (0,0)
major axis=2a=30
a=15
a^2=225
..
Also, from given coordinates of the Foci:
c=9
c^2=81=a^2-b^2
b^2=a^2-c^2=225-81=144
b=12
Equation:
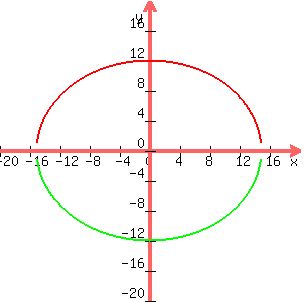
x^2/225+y^2/144=1
see graph below as a visual check on the answers
..
y=±(144-144x^2/225)^.5
|
|
|
| |