Question 460534: what are the foci of the graph x^2/36-y^2/16=1
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The directrix is x=5 and the focus is (11, -7)

The  , by definition, is equidistant from the directrix and the focus. Since , by definition, is equidistant from the directrix and the focus. Since  and and  the midpoint would be at the midpoint would be at  . So the vertex is at ( . So the vertex is at ( , , ) )
If you graph those points you will see the 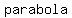 must be on it's side, open to the right. must be on it's side, open to the right.
 would be the would be the  form equation. form equation.
Since  is under the is under the  term, the major axis runs parallel to the term, the major axis runs parallel to the  , and is , and is  units long. units long.


the major axis is  long. long.
Similarly, the minor axis runs parallel to the  and is and is  units long. units long.
If you want to find the location of the 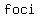 : :
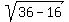
=
=+/-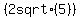
so the 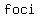 are located at about ( are located at about (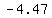 , , ) and ( ) and (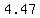 , ,  ) )
|
|
|