SOLUTION: Graph the ellipse. Label the major axis, minor axis, and foci. Please show the graph. 4x^2+3y^2=48

Get it in the form

 if it looks like this ᆼ:

or in the form 

 if it looks like this Ὁ
:

And the way you tell is by the fact that a² is larger than b²



Divide through by 48 to get 1 on the right:



Simplify



Now write x as (x-0) and y as (y-0) 



16 is larger than 12 so the ellipse looks like this: 0
and it is in this form:



Comparing directly gives:

center = (h,k) = (0,0), a² = 16, so a = 4, b² = 12, so b = 

Major axis has length 2a = 2(4) = 8

So we plot the center and draw the major axis 8 units long with
the center (0,0)at its midpoint, which is the green line below 
extending from (0,-4) to (0,4):



Next we'll draw the minor axis 2b = 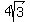 long or about 6.93 
units long with the center (0,0) at its midpoint, which is the blue 
line below extending from (,0) to (,0), 
which is about the points (-1.73,0) to (1.73)



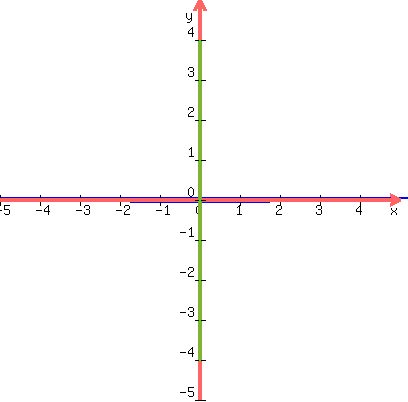and sketch in the ellipse:



To find the focal points, we calculate c from



So the focal points are on the major axis c = w units from the
center:

So they are (0,2) and (0,-2)




Edwin