SOLUTION: write the equation in standard form. name the center, the length of the minor and major axis, and direction. 5x^2+9y^2=720

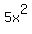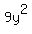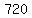
We want to get it in either the form



where the larger denominator a² is under (x-h)² and the smaller
denominator b² is under (y-k)² making the ellipse looks like this 


or the form



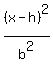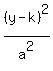where the larger denominator a² is under (y-k)² and the smaller
denominator b² is under (x-h)² making the ellipse looks like this


We get a 1 on the right side, by dividing every term by 720







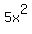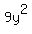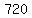
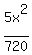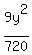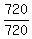
To make it look like



we just need to subtract 0 from x and y



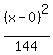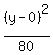So we see the larger denominator is under (x-h)², making the
ellipse look like this 

We compare the two and equate like parts:

h = 0, k = 0, a^2 = 144, b^2 = 80
                                 __    ____     _
So the center is (h,k) = (0,0), the origin.
                __    ____     _ 
a = 12 and b = Ö80 = Ö16*5 = 4Ö5  

a is the semi-major axis and b is the semi-minor axis.

So the entire major axis is 2a = 2*12 = 24 and the 
entire 2b = 2(4Ö5) = 8Ö5

So we see the larger denominator is under (x-h)², making the
ellipse look like this 

Here is the graph



The center is (0,0), the major axis is the width at the widest place,
or 24.  The "direction" is that its major axis is horizontal.


Edwin