SOLUTION: If a circle intersects the hyperbola {{{y = 1/x}}} at four distinct points (x_i, y_i), i = 1,2,3,4, then prove that x_1*x_2 = y_3*y

Click here to see ALL problems on Quadratic-relations-and-conic-sections

Question 390113: If a circle intersects the hyperbola at four distinct points (x_i, y_i), i = 1,2,3,4, then prove that x_1*x_2 = y_3*y_4.
Found 2 solutions by richard1234, robertb:
Answer by richard1234(7193) (Show Source):
You can put this solution on YOUR website!
I'm pretty doubtful this formula works for all circles. This is because if it is true, then switching the order of the points in any way must also produce a true equality.

Note that the points (x_1, y_1)...(x_4, y_4) produces a cyclic quadrilateral. You could use Ptolemy's theorem, which says that if the lengths of the sides of a cyclic quadrilateral are a, b, c, d (in clockwise or counterclockwise order) and the diagonals are e, f, then

I highly doubt this would give a full proof (plus it'd be extremely tedious with lots of algebra because we have to substitute with a value such as 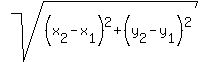--gets ugly very quickly).

An obvious exception is if the center of the circle is at the origin -- this is actually very easy to prove, using symmetry. The function is symmetric about y = x, you can use that in your proof (only if you're given the center of the circle is at the origin).

Answer by robertb(5830) (Show Source):
You can put this solution on YOUR website!
We have to solve the system
,
.
In the equation of the circle above, h, k, and r are all constants. The problem also assures us that the circle and the hyperbola will intersect in 4 distinct points.
Substitute the bottom equation into the top equation: .
Expand the resulting equation:
.
Clear fractions:
.
Combine like terms:
<----(A)
From algebra, we know that for the polynomial
+ ...+ +...+ ,

is equal to the summation of product of the roots of the polynomial taken k at a time. We need this result only for the constant term of (A). We get .
This is the same as , or finally,
.

SOLUTION: If a circle intersects the hyperbola {{{y = 1/x}}} at four distinct points (x_i, y_i), i = 1,2,3,4, then prove that x_1*x_2 = y_3*y_4.

SOLUTION: If a circle intersects the hyperbola {{{y = 1/x}}} at four distinct points (x_i, y_i), i = 1,2,3,4, then prove that x_1x_2 = y_3y_4.