SOLUTION: I am trying to find the y-intercept, as an ordered pair, of the equation {{{ x=3y^2+12y+6 }}}. I have tried solving it myself by making "x" equal to 0 and then I simplified the equ

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: I am trying to find the y-intercept, as an ordered pair, of the equation {{{ x=3y^2+12y+6 }}}. I have tried solving it myself by making "x" equal to 0 and then I simplified the equ      Log On


   

Question 387953: I am trying to find the y-intercept, as an ordered pair, of the equation +x=3y%5E2%2B12y%2B6+. I have tried solving it myself by making "x" equal to 0 and then I simplified the equation to +-%281%2F6%29=y%5E2%2By+, and I was unsure as to what to do after that, or if that was even right. Thank you, and if there was any way that you could show me the steps you took that would be great. Thanks again.
Found 2 solutions by nerdybill, 533908:
Answer by nerdybill(7384) About Me  (Show Source):
You can put this solution on YOUR website!
+x=3y%5E2%2B12y%2B6+
Yes, set x = 0:
+0=3y%5E2%2B12y%2B6+
divide both sides by 3:
+0=y%5E2%2B4y%2B2+
Since you can't factor you must resort to the quadratic formula. Doing so, yields:
y = {-0.586, -3.414}
so, the y-intercepts are at:
(0, -0.586) and (0, -3.414)
.
details of quadratic follows:
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ay%5E2%2Bby%2Bc=0 (in our case 1y%5E2%2B4y%2B2+=+0) has the following solutons:

y%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284%29%5E2-4%2A1%2A2=8.

Discriminant d=8 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-4%2B-sqrt%28+8+%29%29%2F2%5Ca.

y%5B1%5D+=+%28-%284%29%2Bsqrt%28+8+%29%29%2F2%5C1+=+-0.585786437626905
y%5B2%5D+=+%28-%284%29-sqrt%28+8+%29%29%2F2%5C1+=+-3.41421356237309

Quadratic expression 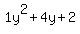1y%5E2%2B4y%2B2 can be factored:
1y%5E2%2B4y%2B2+=+1%28y--0.585786437626905%29%2A%28y--3.41421356237309%29
Again, the answer is: -0.585786437626905, -3.41421356237309. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B4%2Ax%2B2+%29

Answer by 533908(1) About Me  (Show Source):
You can put this solution on YOUR website!
+x=3y%5E2%2B12y%2B6+
Yes, set x = 0:
+0=3y%5E2%2B12y%2B6+
divide both sides by 3:
+0=y%5E2%2B4y%2B2+
Since you can't factor you must resort to the quadratic formula. Doing so, yields:
y = {-0.586, -3.414}
so, the y-intercepts are at:
(0, -0.586) and (0, -3.414)
.