SOLUTION: find the center of an ellipse with the equation 9x^2+16y^2-18x+64y=71 Find the foci of an ellipse with the equation 7(x-2)^2+3(y-2)^2=21

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: find the center of an ellipse with the equation 9x^2+16y^2-18x+64y=71 Find the foci of an ellipse with the equation 7(x-2)^2+3(y-2)^2=21      Log On


   

Question 352315: find the center of an ellipse with the equation 9x^2+16y^2-18x+64y=71

Find the foci of an ellipse with the equation 7(x-2)^2+3(y-2)^2=21
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
To find the center of an ellipse we need the equation in the form:
%28x-h%29%5E2%2Fa%5E2+%2B+%28y-k%29%5E2%2Fb%5E2+=+1 (or with the a's and b's swapped)
In this form the center is (h, k).

To transform the equation we have into the equation we want we will need to complete the squares for both the x terms and the y terms. I'm assuming you have had some practice with this so there will be few comments on it:
9x%5E2%2B16y%5E2-18x%2B64y=71
9x%5E2-18x%2B16y%5E2%2B64y=71
9%28x%5E2-2x%29%2B16%28y%5E2%2B4y%29=71
9%28x%5E2-2x%2B1%29%2B16%28y%5E2%2B4y%2B4%29=71%2B9%2A1%2B16%2A4
(Note we added 9*1 on the right because on the left side we added a 1 inside a parentheses that has a 9 in front of it. And we added a 16*4 on the right because on the left side we added a 4 inside a parentheses that has a 16 in front of it. Getting this right is probably the hardest part of completing squares.)
9%28x%5E2-2x%2B1%29%2B16%28y%5E2%2B4y%2B4%29=71%2B9%2B64
9%28x%5E2-2x%2B1%29%2B16%28y%5E2%2B4y%2B4%29=144
Since the parentheses on the left are perfect squares:
9%28x-1%29%5E2%2B16%28y%2B2%29%5E2=144
9%28x-1%29%5E2%2F144%2B16%28y%2B2%29%5E2%2F144=144%2F144
%28x-1%29%5E2%2F16%2B%28y%2B2%29%5E2%2F9=1
We are very close. We just need a subtraction from y instead of an addition. Rewriting the addition as an equivalent subtraction we get:
%28x-1%29%5E2%2F16%2B%28y-%28-2%29%29%5E2%2F9=1
Now we can "read" the center: (1, -2)

7%28x-2%29%5E2%2B3%28y-2%29%5E2=21
To find the foci we will need the center and the value of "c" (which is the distance from the center to the foci.) For this we will once again need the equation in the form:
%28x-h%29%5E2%2Fa%5E2+%2B+%28y-k%29%5E2%2Fb%5E2+=+1 (or with the a's and b's swapped)
Since we already have the perfect squares, all we need to do is divide both sides by 21:
7%28x-2%29%5E2%2F21%2B3%28y-2%29%5E2%2F21=21%2F21
%28x-2%29%5E2%2F3%2B%28y-2%29%5E2%2F7=1
This makes the center of this ellipse: (2, 2).
In an ellipse, a > b so 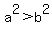a%5E2+%3E+b%5E2. Since 7 > 3, a%5E2+=+7 and b%5E2+=+3. Since the a%5E2 is located under the y terms, this ellipse is a vertically oriented ellipse. And this means that the foci are above and below the center of the ellipse. The value of "c" is far we go up and down from the center to get to the foci. We have a%5E2 and b%5E2 and we can use them and the equation a%5E2+=+b%5E2+%2B+c%5E2 to find c:
7+=+3+%2B+c%5E2
4+=+c%5E2
2+=+c
So we will go up and down 2 from the center. To up from a point, like the center, you add to the y coordinate and to go down you subtract. So the foci will be
(h, k+c) and (h, k-c)
With h = 2, k = 2 and c = 2 we get:
(2, 2+2) and (2, 2-2)
or
(2, 4) and (2, 0)