|
Question 349347: When you use the chain rule to find the slope of a tangent line for the equation x^2+4y^2=4 at point (sqrt(2), -1/sqrt(2)) the slope comes out as m=-1/2 .
When you use implicit differentiation, however, the slope comes out as m=1/2 The back of my textbook states the answer as m=1/2.
Why is m=-1/2 not the correct slope and why does the chain rule give me that answer?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! (Note: If you already read my earlier reply then I have, upon further reflection, figured out how the chain rule could be used on this problem. But it is much harder this way. And since you were unable to get it right this way, perhaps you should stick with the easier method.)
To use the chain rule we need a function which is a composition of functions. Your equation, as I hope you realize, is the equation of an ellipse with its center at the origin. An ellipse is not a function, but the top half and the bottom half of ellipses are functions. So we start by solving your equation for y:
(Note: The zero is there because Algebra.com's software will not let me use the "plus or minus" symbol without a number in front of it.)
This makes  the top half of the ellipse and  the bottom half. Since the point of tangency we are interested in has a negative y coordinate,  , we will use the bottom half. (This may be where you made your mistake.)
Using the chain rule on this we get:
y' =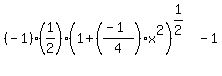 
Simplifying we get:
y' =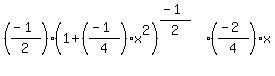 
y' =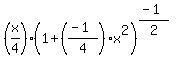 
y' =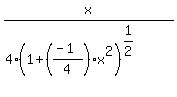 
y' =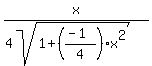 
At this point we can see, since the x at the point of tangency is positive, that our slope will turn out positive. To see what the slope will be, we substitute the given x coordinate,  , into the first derivative:
y' =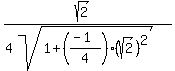 
Simplifying we get:
y' =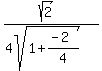 
y' = 
y' =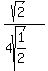 
y' =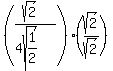 
y' =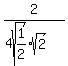 
y' = 
So the slope of the tangent to the ellipse at the point (, ) is 1/2.
|
|
|
| |
