Determine the coordinates of the foci of the original conic in exact form for the equation: 13x^2-6sqroot(3)xy+7y^2-16=0
 The general conic equation is:
The general conic equation is:

 ,
,  ,
,  ,
,  ,
,  ,
,  This is a rotated ellipse because
This is a rotated ellipse because  and
and 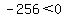 To eliminate the x'y'-term when we rotate through an angle
of
To eliminate the x'y'-term when we rotate through an angle
of  we use the formula
we use the formula
 to find the angle of rotation
to find the angle of rotation  required to eliminate it:
required to eliminate it:




 When we replace
When we replace  by
by  and
and
 by
by 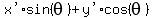 into
into
 using the proper angle of rotation, there will be no x'y' term
and we will get:
using the proper angle of rotation, there will be no x'y' term
and we will get:
 And since D and E are both 0, that simplifies to
And since D and E are both 0, that simplifies to
 The coefficient of
The coefficient of 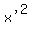 is
is
 The coefficient of
The coefficient of 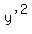 is
is
 So the equation of the ellipse when rotated counter-clockwise 60° is
So the equation of the ellipse when rotated counter-clockwise 60° is
 Getting it in standard form we divide through by 16 to get
1 on the right:
Getting it in standard form we divide through by 16 to get
1 on the right:
 or
or
 Here is the graph. The green axes are the x' and y' axes:
Here is the graph. The green axes are the x' and y' axes:
 Comparing the equation to the standard equation for an ellipse
with center at the origin
Comparing the equation to the standard equation for an ellipse
with center at the origin
 We see that
We see that  or
or  and that
and that  or
or  To find the foci with respect to the x'-y' coordinate system, we
use the Pythagorean relation for ellipses:
To find the foci with respect to the x'-y' coordinate system, we
use the Pythagorean relation for ellipses:




 Thus the foci with respect to the rotated x'y'-coordinate
system are (x',y') = (
Thus the foci with respect to the rotated x'y'-coordinate
system are (x',y') = ( ,0) and (
,0) and ( ,0)
However we must find their coordinates with respect to the
non-rotated original xy-coordinate system.
Let's plot the two foci, which are both
,0)
However we must find their coordinates with respect to the
non-rotated original xy-coordinate system.
Let's plot the two foci, which are both  units from the
origin out on the green x' axis. The x' axis makes a 60° angle with
respect to the x-axis.
units from the
origin out on the green x' axis. The x' axis makes a 60° angle with
respect to the x-axis.
 Now we draw a perpendicular from the focus to the x-axis forming
a right triangle with hypotenuse
Now we draw a perpendicular from the focus to the x-axis forming
a right triangle with hypotenuse  . The horizontal
leg of that right triangle is the x-coordinate of the focus, and
the y-coordinate of that right triangle is the y-coordinate of
the focus.
. The horizontal
leg of that right triangle is the x-coordinate of the focus, and
the y-coordinate of that right triangle is the y-coordinate of
the focus.
 From the right triangle,
From the right triangle,







 So the upper focus is (
So the upper focus is ( ,
, )
and by symmetry the lower focus is (
)
and by symmetry the lower focus is ( ,
, )
Edwin
)
Edwin