|
Question 298194: Write the equation.
Hyperbola with C(-2,0) V(-2,3) y= +/- .5x
I am pretty sure C stands for center and V for vertex. There are two vertices so the second one should be at (-2,-3) I think. I am not sure what to do with the y = +/- .5x though.
Found 2 solutions by Edwin McCravy, Theo:
Answer by Edwin McCravy(20059)   (Show Source):
You can put this solution on YOUR website! Write the equation.
Hyperbola with C(-2,0) V(-2,3) y=±.5(x+2)
[Notice that I had to change your asymptotes' equations, because
the equations you gave (y=±.5x) for asymptotes were not possible
with a hyperbola with center C(-2,0), for the two asymptotes
must intersect at the center of the hyperbola, so I changed
them to have the equations y=±.5(x+2) instead, for either you
copied something wrong, or there was a typo in the book you
got the problem from. But rather than do nothing, I went
ahead and changed the asymptotes.]
First we plot what is given, the vertex, the center, and the two
asymptotes, whose equations are  and 
We see that the hyperbola opens upward and downward.
So we know its standard equation is this:
 , where the center is C(h,k),
and so we know that the center is (-2,0), then h=-2, and k=0.
The center is halway between the vertices, so you are right
that the other vertex is (-2,-3). We plot it:
We connect the vertices to find the transverse axis
We can see that the transverse axis is 6 units long, and since the
transverse axis is  units long, then  and 
Next we draw the top and bottom of the defining rectangle, which
are the horizontal line segments between the two intercepts which
passes through the vertex:
It appears that the corners of the defining rectangle are at
(-8,3), (4,3), (-8,-3), and (4,-3). But we can't just look and see.
We know the y-coordinate of the corners of the defining rectangle
are 3 and -3. So we substitute 3 and -3 for y into each of the asymptotes'
equations:
   
We finish drawing in the defining rectangle, by
drawing its two vertical sides:
Now we can sketch in the hyperbola:
The conjugate axis is along the x-axis, and extends from (-8,0) to (4,0)
Tha conjugate axis has length 12, and since b = one-half of the
conjugate axis's length, b = 6.
Therefore the equation of the hyperbola is
, where h=-2, and k=0, a=3, b=6
 , or
 .
Edwin
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! The general equation for a horizontally oriented hyperbola would be:
The center of your hyperbola is at C = (-2,0).
The vertices of this hyperbola are probably at V1 = (-2,-3) and V2 = (-2,3)
This, I believe, makes this a vertically oriented hyperbola whose general equation would be:
The y = +/- .5x refers to the equation of the asymptotes for the hyperbola.
In a horizontally oriented hyperbola, that equation would be:
y = +/-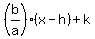 
In a vertically oriented hyperbola, that equation would be:
y = +/-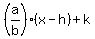 
The distance between the center of the hyperbola and each vertex of the hyperbola is equal to "a".
Since your center is (-2,0) and one of your vertices is at (2,3), then "a" must be equal to 3.
Since the general equation of the asymptotes of a vertically oriented hyperbola is:
y = +/-  and the equation of the asymptotes of your equation is y = +/- 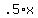 , then the equation of the asymptotes for your hyperbola becomes:
y = +/- .5x = +/-
This makes:
+/- .5x = +/-
The slope of the asymptote on the left side of this equation is +/- .5
The slope of the asymptote on the right side of this equation is +/-  .
Since a = +/- 3, this makes the slope of the asymptote on the right side of this equation equal to 
Because these slopes are just different versions of the slope of the same asymptotes, we can solve for b as follows:
+/- .5 = +/-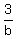 
Multiply both sides of this equation by b to get:
+/- .5b = +/- 3
Multiply both sides of this equation by 2 to get:
+/- b = +/- 6
We now have:
a = 3
b = 6
Since the general form of the equation of our vertically oriented hyperbola is:
, we can replace a^2 with 9 and b^2 with 36 to get:
Since the center of our hyperbola is at (-2,0), and the center of the hyperbola is represented by (h,k), this means that:
h = -2
k = 0
We can replace h and k in the equation of our hyperbola to get:
That's the equation of our hyperbola.
To graph this equation, we have to solve for y.
Solving for y gets us:
y = +/- 
The graph of our equation looks like this:
A more distant view looks like this:
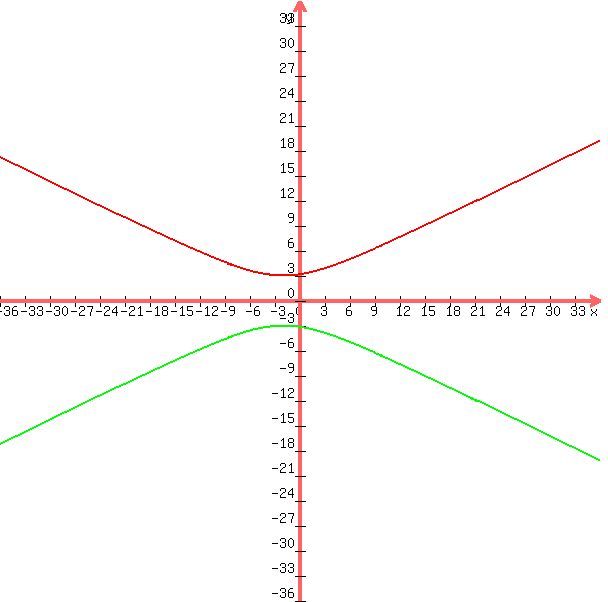
The equation for the asymptotes of this hyperbola are y = +.- .5
We add the equations of those lines to the distant graph to get:
The asymptotes are a little off because we did not account for the center of the hyperbola.
Apparently, the equation y = +/- .5x was the equation for the slope of the asymptotes only.
Since the asymptotes have to go through the center of the hyperbola, we need to modify this equation to account for the fact that the lines are going through the point (-2,0).
The point slope form of the equation of a straight line is (y-y1) = m*(x-x1)
The slope of our line is +/- .5
The point slope form of the equation of the asymptotes of our hyperbola becomes:
(y-y1) = +/- .5*(x-x1)
Since the lines goes through the point (-2,0), then (x1,y1) = (-2,0) and the equation of our asymptotes becomes:
y = +/- .5*(x+2)
We graph these equations of our asymptotes on top of the equation of our hyperbola to get:
Now everything lines up right and the graph clearly shows the asymptotes of the equation of our hyperbola.
You did not need to graph the asymptotes. That's a bonus.
Another bonus is the eccentricity of the hyperbola.
It is given by the equation 
c is the measure of the distance from the center of the hyperbola to one of the foci of the hyperbola.
The value of c is given by the equation 
In this hyperbola, that would make 
The eccentricity of this hyperbola is therefore  = 2.236067978
The higher the eccentricity, the straighter is the hyperbola. A very very high eccentricity would make the hyperbola look more like two parallel lines.
This one is somewhere in the medium range.
"a" and "c" are defined as:
a is the distance from the center of the hyperbola to each vertex.
c is the distance from the center of the hyperbola to each focus.
A pretty decent reference for you to look at is shown below:
http://www.purplemath.com/modules/hyperbola.htm
|
|
|
| |
