|
Question 278068: i'm learning about ellipses and i have the problem:
x squared+4y squared-6x+24y+41=0
i need to find the center, foci, and vertices.
i have no idea how to even start, i tried by first completing the square but i'm missing something because i get confused by that 41 that is thrown in there, please help.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! i'm learning about ellipses and i have the problem:
x squared+4y squared-6x+24y+41=0
i need to find the center, foci, and vertices.
i have no idea how to even start, i tried by first completing the square but i'm missing something because i get confused by that 41 that is thrown in there, please help.
 Get the number on the right by adding
Get the number on the right by adding 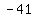 to both sides: to both sides:
 Swap the two middle terms to get the
Swap the two middle terms to get the  -term next to the -term next to the  -term -term
 Multiply the coefficient of x, which is
Multiply the coefficient of x, which is 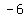 , by , by  ,
get ,
get  then square that number then square that number  which
gives which
gives  Now add
Now add  to both sides: to both sides:
 Since the
Since the  term has a coefficient other than 1,
factor the 4 out of the last two terms on the left: term has a coefficient other than 1,
factor the 4 out of the last two terms on the left:
 Now we complete the square inside the parentheses.
Multiply the coefficient of y, which is
Now we complete the square inside the parentheses.
Multiply the coefficient of y, which is  , by , by  ,
get ,
get  then square that number then square that number 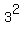 which
gives which
gives 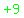 Now we add
Now we add 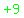 inside the parentheses. However
when we add inside the parentheses. However
when we add  inside the parentheses we are REALLY
adding inside the parentheses we are REALLY
adding 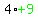 or or  to the left side
because everything in the parentheses is multiplied by the to the left side
because everything in the parentheses is multiplied by the  in front of the parentheses. So we add
in front of the parentheses. So we add  to the right side: to the right side:
 Now we factor the first three terms as
Now we factor the first three terms as 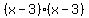 or or  and we factor the three terms inside the parentheses as
and we factor the three terms inside the parentheses as 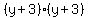 or
or 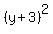 , and combine the numbers on the right as , and combine the numbers on the right as 
 Now to get 1 on the right we divive every term through by 4
Now to get 1 on the right we divive every term through by 4

 Notice that I left a 1 under the bottom of the second term
so that it would be in standard form
Since
Notice that I left a 1 under the bottom of the second term
so that it would be in standard form
Since  is larger than is larger than  and the larger term is under
the and the larger term is under
the 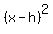 term it is in the form term it is in the form
 and has its major axis horizontal.
and has its major axis horizontal.
 , ,  , ,  , so , so 
 , so , so  , so we plot the center {3,-3) , so we plot the center {3,-3)
 Then we draw the major axis by drawing a horizontal line
Then we draw the major axis by drawing a horizontal line  units both right and left of the center (3,-3)
units both right and left of the center (3,-3)
 Now we can get the vertices, for they are the points ar the ends
of the major axis, and we can see that the major axis, the green
line segment starts at (1,-3) on the left and goes to (5,-3) on
the right, so the vertices are
(1,-3) and (5,-3)
Now we draw the minor axis by drawing a horizontal line
Now we can get the vertices, for they are the points ar the ends
of the major axis, and we can see that the major axis, the green
line segment starts at (1,-3) on the left and goes to (5,-3) on
the right, so the vertices are
(1,-3) and (5,-3)
Now we draw the minor axis by drawing a horizontal line  units both up and down from the center (3,-3):
units both up and down from the center (3,-3):
 Now we can sketch in the ellipse:
Now we can sketch in the ellipse:
 Finally we need to find the foci. The distance from
the center to each focus is
Finally we need to find the foci. The distance from
the center to each focus is  and and  is
calculated by this Pythagorean identity: is
calculated by this Pythagorean identity:



 The coordinates of the foci are
points which are distance of
The coordinates of the foci are
points which are distance of  units right and left of the center on the major axis,
so the two foci are these points:
(3-Ö3,-3) and (3+Ö3,-3)
They are plotted below:
units right and left of the center on the major axis,
so the two foci are these points:
(3-Ö3,-3) and (3+Ö3,-3)
They are plotted below:
 Edwin
Edwin
|
|
|
| |